10 Out Of 21 As A Percentage
listenit
May 25, 2025 · 5 min read
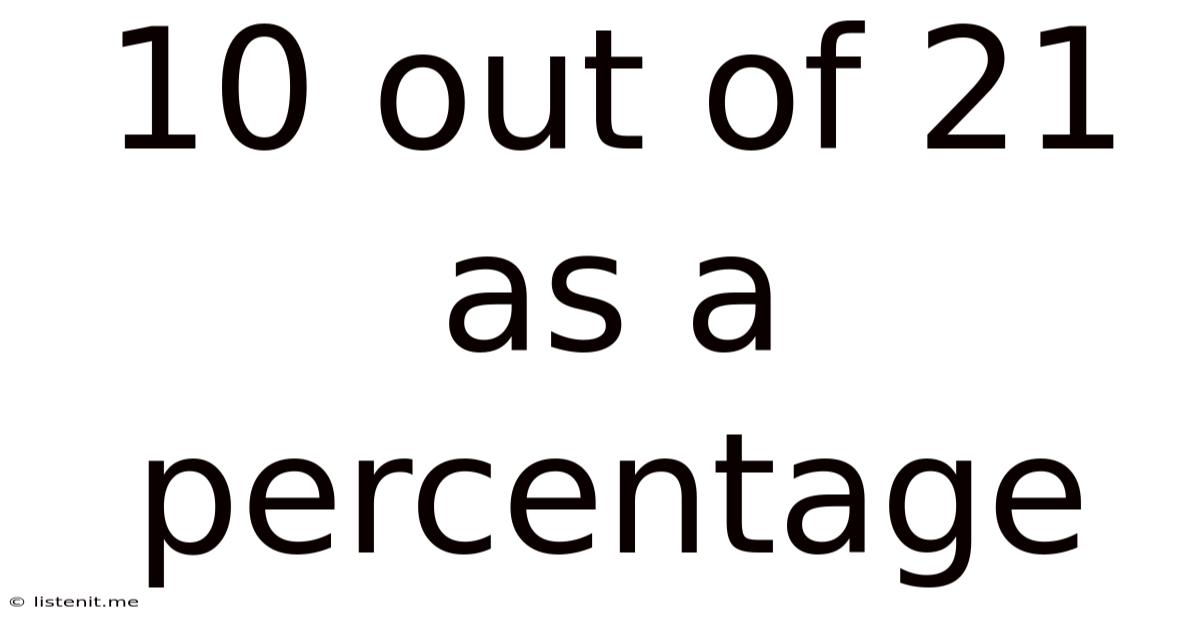
Table of Contents
10 out of 21 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with applications spanning various fields, from everyday budgeting to complex scientific research. Understanding how to convert fractions into percentages is crucial for accurate data interpretation and informed decision-making. This comprehensive guide delves deep into the calculation of "10 out of 21 as a percentage," providing multiple approaches, illustrative examples, and practical applications. We'll also explore the broader context of percentage calculations, offering insights into their significance and diverse uses.
Understanding Percentages
A percentage represents a fraction of 100. The term "percent" literally means "out of one hundred." Therefore, expressing a value as a percentage involves determining what proportion of that value represents one hundredth of the whole. This transformation is vital for comparing different values on a standardized scale.
Calculating 10 out of 21 as a Percentage: The Core Methods
There are several ways to calculate 10 out of 21 as a percentage. We'll outline the most common and effective methods below:
Method 1: The Fraction-to-Percentage Conversion
This is the most straightforward method:
-
Express as a fraction: The phrase "10 out of 21" translates directly into the fraction 10/21.
-
Convert to a decimal: Divide the numerator (10) by the denominator (21): 10 ÷ 21 ≈ 0.476
-
Convert to a percentage: Multiply the decimal by 100: 0.476 × 100 = 47.6%
Therefore, 10 out of 21 is approximately 47.6%.
Method 2: Using Proportions
This method emphasizes the proportional relationship between the parts and the whole:
-
Set up a proportion: We can set up a proportion to solve for the percentage:
10/21 = x/100
Where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiplying gives us:
21x = 1000
-
Solve for x: Divide both sides by 21:
x = 1000/21 ≈ 47.6%
This method confirms our previous result: 10 out of 21 is approximately 47.6%.
Method 3: Utilizing a Calculator
Most calculators have a percentage function. Simply divide 10 by 21 and then multiply the result by 100 to obtain the percentage directly. This method is quick and efficient for everyday calculations.
Practical Applications: Where Percentage Calculations Matter
The ability to calculate percentages is crucial across numerous disciplines and daily scenarios. Here are some notable examples:
1. Academic Performance:
Students frequently encounter percentage calculations when determining their grades. If a student answers 10 out of 21 questions correctly on a test, their score is 47.6%, providing a clear measure of their performance.
2. Financial Management:
Personal and business finances heavily rely on percentage calculations. For example, calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage computations. Understanding these percentages is essential for making informed financial decisions.
3. Data Analysis and Statistics:
Percentages are fundamental to statistical analysis. They are used to represent proportions within datasets, enabling meaningful comparisons and interpretations of trends and patterns. In research, percentages often express the prevalence of certain characteristics or outcomes within a population.
4. Sales and Marketing:
Businesses extensively use percentages in sales, marketing, and advertising. Calculating sales growth, conversion rates, market share, and discount offers all depend on accurately determining percentages. Marketing campaigns often evaluate their success using percentage-based metrics.
5. Healthcare and Medicine:
Percentage calculations are prevalent in healthcare settings. For example, determining the effectiveness of a treatment, calculating the success rate of a surgical procedure, or representing the prevalence of a disease within a population all require accurate percentage calculations.
6. Engineering and Construction:
Engineers and contractors use percentages for various calculations, including material estimations, project completion progress, and tolerance levels in design specifications. Accurate percentage calculations ensure the smooth execution of projects.
7. Everyday Life:
Even in our everyday lives, percentages are encountered constantly. Calculating tips at restaurants, determining discounts during sales, understanding interest rates on loans, and interpreting statistics presented in news reports are all applications of percentage calculations.
Beyond the Basics: Advanced Percentage Calculations
While calculating 10 out of 21 is relatively straightforward, more complex percentage problems may arise. Here are some advanced scenarios:
Calculating Percentage Change:
This involves determining the percentage increase or decrease between two values. The formula is:
[(New Value - Old Value) / Old Value] × 100
For example, if sales increased from 20 units to 30 units, the percentage increase would be:
[(30 - 20) / 20] × 100 = 50%
Calculating Percentage of a Percentage:
This involves finding a percentage of a percentage. For instance, finding 20% of 50% would be:
(20/100) × (50/100) × 100 = 10%
Solving Percentage Problems with Unknown Values:
Some problems might present unknowns, requiring algebraic techniques to solve for the missing percentage or value. For example, "What number is 47.6% of 21?" requires solving the equation:
x = 0.476 × 21
This gives x ≈ 10, demonstrating the reverse calculation.
Error Handling and Rounding
When working with percentages, it's essential to be mindful of potential rounding errors. Depending on the context, it might be necessary to round the percentage to a specific number of decimal places to ensure accuracy and clarity. For instance, 47.6% could be rounded to 48% for simpler communication, but retaining the decimal place might be crucial for scientific or financial applications demanding higher precision.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, such as "10 out of 21 as a percentage," is a valuable skill applicable across a wide array of situations. From simple everyday tasks to complex data analysis, the ability to convert fractions into percentages accurately ensures informed decision-making and a deeper comprehension of numerical information. Mastering these calculations enhances your problem-solving abilities and improves your proficiency in various fields, contributing to better comprehension and performance in academic, professional, and personal life. Remember to choose the calculation method that best suits your needs and context, paying close attention to accuracy and rounding to achieve the desired level of precision.
Latest Posts
Latest Posts
-
What Size Tyres Fit My Rims
May 25, 2025
-
Highest Common Factor Of 2 And 8
May 25, 2025
-
1947 To 2023 How Many Years
May 25, 2025
-
What Is 10 Of 10 Dollars
May 25, 2025
-
13 15 Divided By 7 10
May 25, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.