7 Divided By 9 As A Fraction
listenit
May 25, 2025 · 5 min read
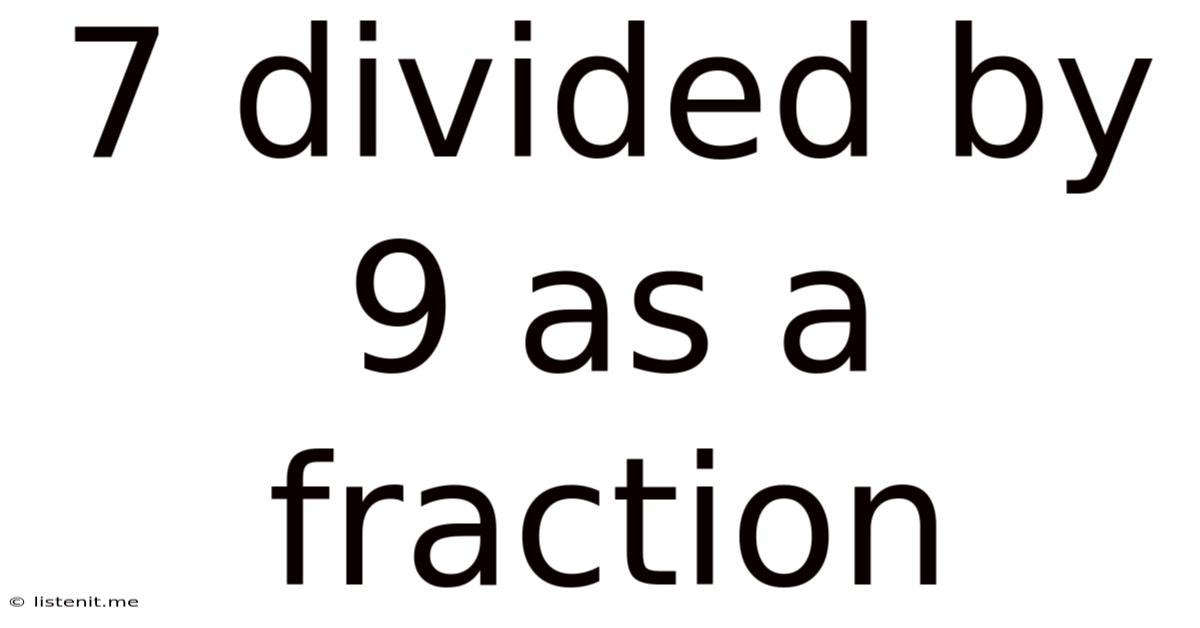
Table of Contents
7 Divided by 9 as a Fraction: A Comprehensive Guide
Understanding fractions is a fundamental concept in mathematics, crucial for various applications from everyday calculations to complex scientific equations. This article delves deep into the seemingly simple problem of dividing 7 by 9, transforming it into its fractional representation and exploring related concepts. We'll cover not only the basic conversion but also delve into the practical implications and explore various ways to represent and manipulate this fraction.
Understanding Division and Fractions
Before diving into the specifics of 7 divided by 9, let's solidify the connection between division and fractions. Division essentially asks, "How many times does one number fit into another?" Fractions, on the other hand, represent parts of a whole. The numerator (top number) represents the number of parts we have, and the denominator (bottom number) represents the total number of equal parts the whole is divided into.
Therefore, dividing 7 by 9 can be interpreted as: "How many parts of size 9 fit into 7?" Since 9 is larger than 7, the answer will be less than 1, representing a fraction.
Converting 7 Divided by 9 into a Fraction
The process of converting 7 divided by 9 into a fraction is straightforward:
- The dividend (7) becomes the numerator. This is the number being divided.
- The divisor (9) becomes the denominator. This is the number we're dividing by.
Therefore, 7 divided by 9 as a fraction is simply 7/9.
This fraction is already in its simplest form because 7 and 9 share no common factors other than 1. In other words, they are coprime.
Representing 7/9 in Different Forms
While 7/9 is the simplest and most common representation, we can also explore other ways to represent this fraction to enhance understanding and facilitate calculations in different contexts.
Decimal Representation
Converting 7/9 to a decimal involves performing the division: 7 ÷ 9 = 0.7777... This is a repeating decimal, often denoted as 0.7̅ or 0.77̅7. The bar over the 7 indicates that the digit 7 repeats infinitely.
Percentage Representation
To express 7/9 as a percentage, we multiply the decimal representation by 100: 0.7̅ × 100 ≈ 77.78%. This means that 7/9 represents approximately 77.78% of a whole.
Practical Applications of 7/9
Understanding and working with fractions like 7/9 is crucial in various real-world scenarios. Here are some examples:
-
Measurement and Proportion: Imagine you have a 9-meter long rope and you need a piece that's 7 meters long. The fraction 7/9 represents the proportion of the rope you need.
-
Baking and Cooking: Recipes often involve fractional amounts of ingredients. If a recipe calls for 7/9 of a cup of sugar, you'll need to accurately measure this quantity.
-
Probability and Statistics: Probability is often expressed as a fraction. If there's a 7 out of 9 chance of an event occurring, the probability is 7/9.
-
Data Analysis: Representing data using fractions can help simplify complex information and provide insights into proportions and trends.
Manipulating 7/9 in Calculations
Working with fractions requires understanding various operations. Here's how we can manipulate 7/9:
Adding and Subtracting Fractions
To add or subtract fractions, they must have a common denominator. For example, to add 7/9 and 2/9, we simply add the numerators: 7/9 + 2/9 = 9/9 = 1. If the denominators are different, you need to find the least common multiple (LCM) and adjust the fractions accordingly.
Multiplying Fractions
Multiplying fractions is straightforward; multiply the numerators together and the denominators together: (7/9) × (2/3) = (7 × 2) / (9 × 3) = 14/27.
Dividing Fractions
Dividing fractions involves inverting (flipping) the second fraction and then multiplying: (7/9) ÷ (2/3) = (7/9) × (3/2) = 21/18 = 7/6. Notice that we simplified the resulting fraction.
Approximating 7/9
In certain situations, an approximation of 7/9 might be sufficient. Since 7/9 ≈ 0.78, we can round it to 0.8 or even 1, depending on the level of accuracy required. The context dictates the level of precision needed.
Comparing 7/9 to Other Fractions
Understanding how 7/9 relates to other fractions can be helpful in various contexts. For example, comparing it to 1/2 (0.5) shows that 7/9 is larger, while comparing it to 4/5 (0.8) shows it's smaller. This comparative analysis provides context and helps in decision-making processes.
Advanced Concepts Related to 7/9
The seemingly simple fraction 7/9 opens doors to more advanced mathematical concepts:
-
Continued Fractions: 7/9 can be expressed as a continued fraction, providing an alternative representation and insights into its properties.
-
Convergents: Approximations of 7/9 using continued fractions can lead to finding convergents, which are rational numbers that closely approximate the original fraction.
Conclusion: Mastering the Fundamentals
Understanding the fraction 7/9, seemingly basic, allows you to build a strong foundation in fractions and their applications. Through exploring different representations, manipulations, and comparisons, we've unveiled the versatility and significance of this simple fraction. Whether it's in everyday life, scientific calculations, or advanced mathematical pursuits, mastering fractional concepts is essential for success. Remember, a solid understanding of basic arithmetic concepts like this forms the bedrock of more complex mathematical reasoning and problem-solving abilities. The more you practice and explore, the more confident and proficient you will become in handling fractions and other mathematical concepts.
Latest Posts
Latest Posts
-
What Are Mortgage Payments On 150 000
May 25, 2025
-
53k A Year Is How Much A Month
May 25, 2025
-
What Is 1 3 Of 54
May 25, 2025
-
What Is The Greatest Common Factor Of 18 And 54
May 25, 2025
-
How Many Hours Is 15 Years
May 25, 2025
Related Post
Thank you for visiting our website which covers about 7 Divided By 9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.