What Is The Square Root Of 87
listenit
Mar 28, 2025 · 6 min read
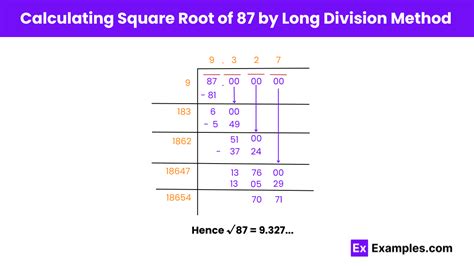
Table of Contents
What is the Square Root of 87? A Deep Dive into Calculation and Applications
The seemingly simple question, "What is the square root of 87?" opens a door to a fascinating world of mathematical concepts and practical applications. While a simple calculator can provide a decimal approximation, understanding the process and implications of finding the square root of 87 offers far greater insight. This article will explore various methods of calculating the square root of 87, discuss its significance in different fields, and delve into related mathematical concepts.
Understanding Square Roots
Before we tackle the square root of 87 specifically, let's establish a foundational understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. In simpler terms, it's the inverse operation of squaring a number. For instance, the square root of 25 is 5 because 5 * 5 = 25. This relationship is often represented as √25 = 5.
Calculating the Square Root of 87: Methods and Approaches
87 isn't a perfect square; there's no whole number that, when multiplied by itself, equals 87. This means we'll need to employ methods to approximate its square root. Here are a few approaches:
1. Using a Calculator
The simplest and most direct method is using a calculator. Most calculators have a square root function (√). Simply input 87 and press the square root button. The result will be approximately 9.327379. This is a decimal approximation, as the square root of 87 is an irrational number – it cannot be expressed as a simple fraction.
2. The Babylonian Method (or Heron's Method)
This iterative method provides increasingly accurate approximations of square roots. It works by repeatedly refining an initial guess. Here's how it works for √87:
-
Make an initial guess: Let's guess 9 (since 9² = 81, which is close to 87).
-
Improve the guess: Divide 87 by the initial guess (87/9 ≈ 9.667).
-
Average: Average the initial guess and the result from step 2: (9 + 9.667)/2 ≈ 9.3335.
-
Repeat: Use this average as the new guess and repeat steps 2 and 3. With each iteration, the approximation becomes more precise. After several iterations, you'll converge on a value very close to the calculator's result.
3. Long Division Method
While more complex than the Babylonian method, the long division method for finding square roots offers a deeper understanding of the underlying mathematical process. This method involves a series of steps involving estimation, subtraction, and bringing down digits, similar to long division for arithmetic. The process is quite involved and better explained visually with diagrams, but the result will again approximate 9.327.
The Significance of Irrational Numbers: Why √87 is Important
The fact that √87 is an irrational number is significant. Irrational numbers are numbers that cannot be expressed as a ratio of two integers (a fraction). Their decimal representations neither terminate nor repeat. This seemingly abstract property has profound implications across various fields:
-
Geometry: Irrational numbers often arise in geometric calculations. For example, the diagonal of a square with sides of length 1 is √2, an irrational number. Similarly, many calculations involving circles and spheres involve π (pi), another irrational number. The square root of 87 might represent the length of a diagonal or other geometric relationship in a complex shape.
-
Physics: Many physical phenomena involve irrational numbers. The period of a pendulum, for instance, involves square roots. Calculations involving wave functions and quantum mechanics also frequently involve irrational numbers, including square roots.
-
Engineering: Precision engineering and design often require calculations involving irrational numbers. This includes calculations of stress, strain, and material properties, as well as the design of intricate structures and systems. Approximations are often used in practical applications, but a deep understanding of irrational numbers is crucial for accuracy and optimization.
-
Computer Science: Algorithms and data structures often depend on the efficient representation and manipulation of numbers, including irrational numbers. While computers cannot store irrational numbers precisely, approximations are used extensively in scientific computing, simulations, and graphical rendering.
Applications of Square Roots and √87
The square root function, and specifically the approximation of √87, has numerous practical applications:
-
Right-Angled Triangles (Pythagorean Theorem): The Pythagorean theorem (a² + b² = c²) is fundamental to geometry and trigonometry. If you know the lengths of two sides of a right-angled triangle, you can use the square root to calculate the length of the third side. For example, if a=6 and b=7, then c = √(6² + 7²) ≈ √85, close to √87.
-
Area Calculations: The area of many geometric shapes involves square roots. The area of a regular octagon, for instance, depends on the square root of complex expressions. Similarly, more advanced geometric computations often involve the calculation of square roots.
-
Statistics: Standard deviation and variance calculations in statistics utilize square roots. These are vital measures in data analysis, used to understand the spread or dispersion of data around the mean. Understanding square roots is essential for interpreting statistical results.
-
Financial Modeling: Square roots are used in financial modeling, for instance, in calculating volatility and risk assessment in investment portfolios.
Advanced Concepts Related to Square Roots of 87
Understanding the square root of 87 extends beyond basic calculation. It opens doors to more complex mathematical concepts:
-
Series Expansions: Irrational numbers like √87 can be expressed using infinite series, such as Taylor series or binomial series. These series provide increasingly accurate approximations of the square root as more terms are included.
-
Numerical Analysis: Numerical analysis deals with approximating solutions to mathematical problems. Various numerical techniques exist for accurately approximating √87 to a desired level of precision. These methods are important for solving equations and performing simulations where exact solutions are unavailable.
-
Complex Numbers: The concept of square roots extends to complex numbers, which involve both real and imaginary parts (represented using "i," where i² = -1). While not directly applicable to the real number √87, the understanding of square roots underpins the broader concept of complex number analysis.
Conclusion: The Enduring Importance of √87
While a simple calculator quickly provides an approximation of the square root of 87 (approximately 9.327), exploring the underlying methods and understanding the significance of irrational numbers significantly enriches our mathematical knowledge. The calculation of √87 is not merely an isolated mathematical exercise but a gateway to understanding deeper mathematical concepts and their practical applications in various fields. From geometry and physics to engineering and finance, the ability to work with square roots and understand their implications is crucial for solving problems and advancing our understanding of the world around us. The seemingly simple question "What is the square root of 87?" thus reveals a rich tapestry of mathematical insights.
Latest Posts
Latest Posts
-
The Least Common Multiple Of 6 And 9
Mar 31, 2025
-
6 1 2 As An Improper Fraction
Mar 31, 2025
-
How Do Sedimentary Rocks Change Into Igneous Rocks
Mar 31, 2025
-
The Sum Of 3 Consecutive Integers
Mar 31, 2025
-
Is Benzene A Pure Substance Or Mixture
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 87 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
