The Least Common Multiple Of 6 And 9
listenit
Mar 31, 2025 · 5 min read
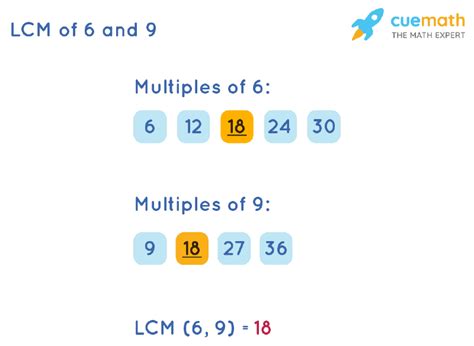
Table of Contents
The Least Common Multiple (LCM) of 6 and 9: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods for calculating it offers valuable insights into number theory and its practical applications. This article delves deep into finding the LCM of 6 and 9, exploring various approaches, and demonstrating their broader relevance in mathematics and beyond.
Understanding Least Common Multiples
Before we tackle the specific case of 6 and 9, let's establish a solid understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers as factors. This concept is crucial in various areas, from simplifying fractions to scheduling events.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: It's divisible by all the given integers.
- Smallest Value: It is the smallest positive integer satisfying the divisibility condition.
Methods for Calculating LCM(6, 9)
Several methods exist for determining the LCM of two or more numbers. Let's explore three common and effective approaches:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48...
Multiples of 9: 9, 18, 27, 36, 45, 54...
By comparing the lists, we can see that the smallest common multiple is 18. This method is simple but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 6: 2 × 3
- Prime factorization of 9: 3 × 3 = 3²
To find the LCM, we take the highest power of each prime factor present in either factorization:
LCM(6, 9) = 2 × 3² = 2 × 9 = 18
This method is more systematic and generally faster than listing multiples, particularly for larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are related through the following formula:
LCM(a, b) × GCD(a, b) = a × b
First, we find the GCD of 6 and 9 using the Euclidean algorithm or prime factorization.
- Prime factorization of 6: 2 × 3
- Prime factorization of 9: 3²
The common prime factor is 3, and the lowest power is 3¹. Therefore, GCD(6, 9) = 3.
Now, we can use the formula:
LCM(6, 9) = (6 × 9) / GCD(6, 9) = 54 / 3 = 18
This method is particularly useful when dealing with larger numbers where finding the prime factorization might be computationally expensive. The Euclidean algorithm for finding the GCD is efficient even for very large numbers.
Real-World Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various fields:
1. Scheduling and Time Management
Imagine you have two machines that run cycles of 6 minutes and 9 minutes respectively. To determine when both machines will complete a cycle simultaneously, you need to find the LCM(6, 9). The LCM, 18, indicates that both machines will finish a cycle together every 18 minutes. This principle is applicable in scheduling meetings, production cycles, and other timed events.
2. Fraction Arithmetic
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator. This simplifies the process of adding or subtracting the fractions.
3. Gear Ratios and Mechanical Systems
In mechanical engineering, the LCM is used to calculate gear ratios and synchronization in complex mechanical systems. Ensuring components operate in harmony often requires understanding the LCM of their respective cycles or speeds.
4. Music Theory and Rhythm
Musical rhythms and note durations often involve fractions and multiples. The LCM is crucial in determining when different rhythmic patterns will align, helping composers create complex and harmonious musical pieces.
Expanding the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method remains particularly efficient. For example, to find the LCM of 6, 9, and 12:
- Prime factorization of 6: 2 × 3
- Prime factorization of 9: 3²
- Prime factorization of 12: 2² × 3
The LCM(6, 9, 12) = 2² × 3² = 4 × 9 = 36
Conclusion: The Importance of Understanding LCM
The seemingly simple concept of the least common multiple holds significant weight in various mathematical and real-world applications. Understanding the different methods for calculating the LCM, from listing multiples to using prime factorization and the GCD, equips you with valuable problem-solving skills. The ability to efficiently determine the LCM is not just a mathematical skill; it’s a crucial tool for tackling problems in diverse fields, emphasizing the interconnectedness of mathematical concepts and their practical relevance. The example of LCM(6, 9) = 18 serves as a foundational stepping stone for understanding more complex LCM calculations and their broader impact on various disciplines. Mastering the LCM is key to mastering many facets of mathematics and its practical applications.
Latest Posts
Latest Posts
-
Why Are Hydrogen Bonds Important For Life
Apr 01, 2025
-
How Many Oz In Quarter Pound
Apr 01, 2025
-
How Many Cc In 10 Ml
Apr 01, 2025
-
Number Of Valence Electrons For Silicon
Apr 01, 2025
-
What Is The Area Of This Circle In Square Centimeters
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about The Least Common Multiple Of 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
