What Is The Square Root Of 59
listenit
Apr 03, 2025 · 4 min read
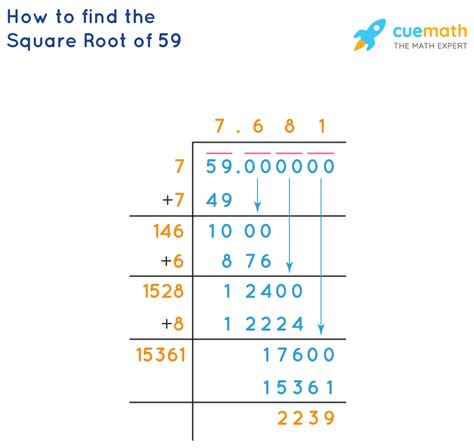
Table of Contents
What is the Square Root of 59? A Deep Dive into Irrational Numbers and Approximation Techniques
The question, "What is the square root of 59?" might seem simple at first glance. However, delving into this seemingly straightforward mathematical problem reveals a fascinating journey into the world of irrational numbers and the various methods used to approximate their values. Unlike the square root of perfect squares (like 16, which is 4 x 4, or 25 which is 5 x 5), the square root of 59 doesn't yield a neat, whole number answer. It's an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Understanding Irrational Numbers
Before we explore methods to approximate √59, let's briefly revisit the concept of irrational numbers. These numbers cannot be expressed as the ratio of two integers (a fraction). Their decimal representation is non-terminating and non-repeating. Famous examples include π (pi) and e (Euler's number), both fundamental constants in mathematics and science. The square root of any non-perfect square is also irrational. This is why finding the exact value of √59 is impossible; we can only find increasingly accurate approximations.
Methods for Approximating √59
Several techniques can provide increasingly precise approximations of √59. Let's explore some of the most common and effective approaches:
1. Using a Calculator
The simplest way to obtain an approximation of √59 is by using a calculator or computer software. These tools utilize sophisticated algorithms to calculate square roots to a high degree of accuracy. A standard calculator will typically display √59 as approximately 7.68114574787. The level of precision depends on the calculator's capabilities.
2. The Babylonian Method (or Heron's Method)
This iterative method provides a progressively more accurate approximation with each iteration. It's based on an ancient algorithm and remarkably efficient. Here's how it works:
-
Make an initial guess: Start with an educated guess. Since 7² = 49 and 8² = 64, a reasonable initial guess for √59 would be 7.5.
-
Iterate: Apply the following formula repeatedly:
x<sub>n+1</sub> = 0.5 * (x<sub>n</sub> + (59/x<sub>n</sub>))
Where:
- x<sub>n</sub> is the current guess
- x<sub>n+1</sub> is the next, improved guess
-
Repeat: Continue iterating using the newly calculated value as the next guess. The closer your guess gets to the actual square root, the smaller the difference between successive iterations will become.
Let's demonstrate a few iterations:
- Iteration 1: x<sub>1</sub> = 0.5 * (7.5 + (59/7.5)) ≈ 7.6667
- Iteration 2: x<sub>2</sub> = 0.5 * (7.6667 + (59/7.6667)) ≈ 7.6811
- Iteration 3: x<sub>3</sub> = 0.5 * (7.6811 + (59/7.6811)) ≈ 7.6811457
As you can see, the approximation converges rapidly towards the actual value. After just a few iterations, we achieve a high degree of accuracy.
3. The Digit-by-Digit Method (Long Division for Square Roots)
This method is a manual technique that systematically reveals the digits of the square root. It's more laborious than the Babylonian method but offers a deeper understanding of the process. The full explanation is quite involved, but the core idea is to successively subtract strategically chosen multiples of 10, 100, 1000, etc., from the number and determine the corresponding digits of the square root.
4. Using Continued Fractions
Continued fractions provide another elegant way to represent irrational numbers. They express a number as a sum of fractions where the denominators themselves are fractions. While calculating the continued fraction representation of √59 is complex, it converges towards the actual value, offering a unique perspective on approximating the square root.
The Significance of Irrational Numbers
Understanding the concept of irrational numbers and methods for their approximation has significant implications across various fields:
-
Mathematics: Irrational numbers are fundamental to many mathematical concepts and proofs, forming the backbone of calculus and advanced mathematical analysis.
-
Physics: Constants like π and e appear frequently in physics equations, governing phenomena from planetary orbits to radioactive decay. Accurate approximations are essential for making accurate predictions and calculations.
-
Engineering: Precise estimations are critical in engineering design, where accuracy is paramount. Whether designing bridges, circuits, or algorithms, the ability to handle irrational numbers accurately is essential.
-
Computer Science: Algorithms for approximating irrational numbers are crucial in computer graphics, numerical analysis, and simulations. Efficient algorithms improve computational speed and precision.
Conclusion: More than Just a Number
The seemingly simple question, "What is the square root of 59?", opens a door to a richer understanding of irrational numbers, approximation techniques, and their importance across diverse scientific and technological disciplines. Whether you use a calculator, apply the Babylonian method, or delve into the intricacies of continued fractions, the pursuit of approximating √59 provides valuable insights into the fascinating world of mathematics and its profound applications. The journey towards finding even a close approximation highlights the fundamental limitations of representing certain mathematical concepts precisely and the power of approximation techniques in bridging this gap. The value itself, approximately 7.6811, is only a starting point for a much deeper exploration.
Latest Posts
Latest Posts
-
In What Organelle Does Cellular Respiration Occur In
Apr 04, 2025
-
How Many Electrons Are In Bromine
Apr 04, 2025
-
Which Organelle Does Cellular Respiration Occur In
Apr 04, 2025
-
Lewis Structure For N Ch3 3
Apr 04, 2025
-
How Many Feet Is A Marathon
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 59 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
