What Is The Square Root Of 243
listenit
Mar 31, 2025 · 5 min read
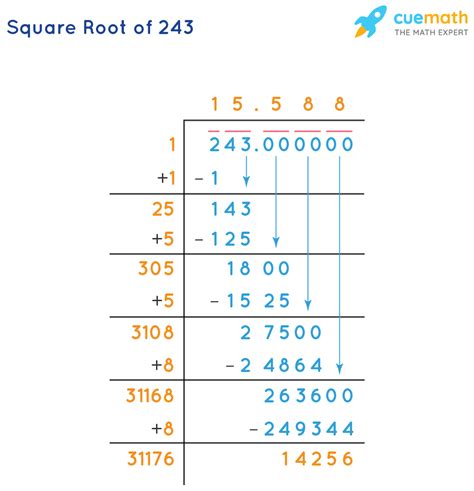
Table of Contents
What is the Square Root of 243? A Deep Dive into Square Roots and Simplification
The question, "What is the square root of 243?" seems simple at first glance. However, understanding the answer fully requires delving into the fascinating world of square roots, prime factorization, and simplifying radical expressions. This comprehensive guide will not only answer the question directly but also equip you with the knowledge to tackle similar problems with confidence.
Understanding Square Roots
Before we tackle the square root of 243, let's establish a firm understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. We denote the square root using the radical symbol (√).
Key Concepts:
- Perfect Squares: These are numbers that result from squaring an integer (e.g., 9, 16, 25, 36). The square roots of perfect squares are whole numbers.
- Non-Perfect Squares: These are numbers that do not result from squaring an integer (e.g., 2, 3, 7, 243). Their square roots are irrational numbers – meaning they cannot be expressed as a simple fraction and their decimal representation goes on forever without repeating.
- Simplifying Radicals: This process involves reducing a square root to its simplest form by factoring out perfect squares from the radicand (the number inside the square root).
Finding the Square Root of 243: A Step-by-Step Approach
243 is not a perfect square. Therefore, its square root will be an irrational number. To simplify it, we'll use prime factorization.
1. Prime Factorization of 243:
We break down 243 into its prime factors. Prime factors are numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11).
- 243 is divisible by 3: 243 = 3 x 81
- 81 is also divisible by 3: 81 = 3 x 27
- 27 is divisible by 3: 27 = 3 x 9
- 9 is divisible by 3: 9 = 3 x 3
Therefore, the prime factorization of 243 is 3 x 3 x 3 x 3 x 3 = 3<sup>5</sup>
2. Simplifying the Square Root:
Now, we rewrite the square root of 243 using the prime factorization:
√243 = √(3<sup>5</sup>)
We look for pairs of identical factors within the radicand. Each pair can be brought out of the square root as a single factor.
√(3<sup>5</sup>) = √(3<sup>2</sup> x 3<sup>2</sup> x 3) = √(3<sup>2</sup>) x √(3<sup>2</sup>) x √3 = 3 x 3 x √3 = 9√3
Therefore, the simplified square root of 243 is 9√3
Understanding Irrational Numbers and Decimal Approximations
As mentioned earlier, the square root of 243 is an irrational number. This means its decimal representation is non-terminating and non-repeating. However, we can find an approximation using a calculator:
√243 ≈ 15.588
This approximation is useful for practical applications where a precise value isn't strictly necessary. However, remember that 9√3 is the exact, simplified form.
Practical Applications of Square Roots
Square roots have widespread applications in various fields:
- Geometry: Calculating the diagonal of a square, the hypotenuse of a right-angled triangle (using the Pythagorean theorem), and the area of a circle are just a few examples.
- Physics: Many physical formulas involve square roots, such as calculations related to velocity, acceleration, and energy.
- Engineering: Engineers use square roots in structural calculations, designing bridges, buildings, and other structures.
- Computer Graphics: Square roots are essential in 3D graphics programming for calculations involving vectors and distances.
- Finance: Square roots are used in financial calculations, such as determining standard deviation and variance in investments.
Advanced Concepts Related to Square Roots
1. Complex Numbers: The square root of a negative number is not a real number. It belongs to the set of complex numbers, which involves the imaginary unit 'i', where i<sup>2</sup> = -1. For example, √-243 = √(-1 x 243) = i√243 = 9i√3
2. nth Roots: The concept of square roots extends to higher-order roots. For example, the cube root (3√) is a value that, when multiplied by itself three times, equals the original number. Similarly, you can have fourth roots, fifth roots, and so on.
3. Radical Equations: These are equations that contain variables within radicals. Solving radical equations often involves squaring both sides of the equation to eliminate the radical.
4. Rationalizing the Denominator: When a radical expression has a radical in the denominator, it's often necessary to rationalize the denominator by multiplying the numerator and denominator by a suitable expression to remove the radical from the denominator.
Conclusion: Mastering Square Roots
Understanding the square root of 243 goes beyond simply finding a numerical approximation. It's about grasping the fundamental concepts of square roots, prime factorization, and simplifying radical expressions. This knowledge is not just academically valuable; it forms the basis for numerous applications across various disciplines. By mastering these concepts, you can confidently tackle more complex mathematical problems and appreciate the elegance and power of mathematical principles. Remember, the simplified form, 9√3, provides the exact and most mathematically correct answer, while decimal approximations offer practical values for specific applications. This deep dive has provided a solid foundation to build upon your understanding of square roots, allowing you to solve similar problems with increased proficiency.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 24 And 42
Apr 02, 2025
-
What 3 Particles Make Up An Atom
Apr 02, 2025
-
Blood Is What Type Of Mixture
Apr 02, 2025
-
What Is The Empirical Formula Of Ibuprofen
Apr 02, 2025
-
What Is One Sixth As A Decimal
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 243 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
