What Is The Square Root Of 105
listenit
Apr 02, 2025 · 5 min read
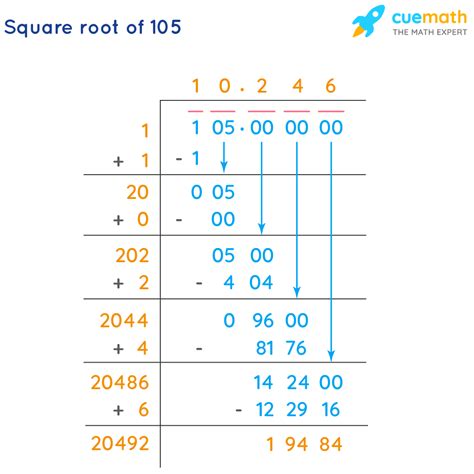
Table of Contents
What is the Square Root of 105? A Deep Dive into Calculation and Applications
The seemingly simple question, "What is the square root of 105?" opens a door to a fascinating exploration of mathematics, encompassing various calculation methods, practical applications, and the broader context of numerical analysis. While a calculator readily provides an approximate decimal value, understanding the underlying principles and exploring alternative approaches offers a richer appreciation of the concept.
Understanding Square Roots
Before delving into the specifics of the square root of 105, let's solidify our understanding of square roots. The square root of a number is a value that, when multiplied by itself (squared), equals the original number. For instance, the square root of 9 is 3 because 3 x 3 = 9. This relationship is often represented mathematically as √105, where the symbol '√' denotes the square root operation.
Calculating the Square Root of 105: Methods and Approaches
Unlike perfect squares (numbers with integer square roots like 9, 16, 25, etc.), 105 doesn't have a whole number square root. This means its square root is an irrational number – a number that cannot be expressed as a simple fraction and continues infinitely without repeating. Let's explore several methods to approximate its value:
1. Using a Calculator: The Easiest Approach
The most straightforward method is using a calculator. Simply input √105, and the calculator will display an approximate decimal value, typically around 10.247. This is a convenient method for quick estimations, but it doesn't provide insight into the underlying mathematical process.
2. Babylonian Method (or Heron's Method): An Iterative Approach
The Babylonian method is an ancient algorithm for approximating square roots. It's an iterative process, meaning it refines the approximation with each step. Here's how it works for √105:
-
Start with an initial guess: Let's guess 10.
-
Improve the guess: Divide 105 by the guess (105/10 = 10.5).
-
Average: Average the result from step 2 with the initial guess: (10 + 10.5)/2 = 10.25.
-
Repeat: Use 10.25 as the new guess and repeat steps 2 and 3. (105/10.25 ≈ 10.2439) (10.25 + 10.2439)/2 ≈ 10.247
-
Iterate until desired accuracy: Continue this process until the difference between successive approximations is smaller than the desired level of accuracy. The more iterations, the closer the approximation gets to the actual value.
This method, while more involved than using a calculator, provides a deeper understanding of how numerical approximations are made.
3. Using Logarithms: A Less Common but Powerful Method
Logarithms can be used to calculate square roots, though it's generally less intuitive than the Babylonian method. The process relies on the logarithmic property that log(√x) = ½log(x).
-
Find the logarithm of 105 (using a logarithm table or calculator).
-
Divide the result by 2.
-
Find the antilogarithm of the result from step 2.
This method leverages the properties of logarithms to simplify the calculation, making it useful in specific contexts where logarithmic computations are already being used.
4. Linear Approximation: A Simple Estimation
For a rough estimate, we can use linear approximation. We know that √100 = 10 and √121 = 11. Since 105 lies between 100 and 121, its square root should be between 10 and 11. A simple linear interpolation can provide a reasonable approximation.
The difference between 121 and 100 is 21, and 105 is 5 units away from 100. Therefore, a rough estimate is 10 + (5/21) ≈ 10.24.
This method is useful for quick, back-of-the-envelope calculations where high precision isn't required.
Applications of the Square Root of 105 and Similar Calculations
The calculation and understanding of square roots, particularly irrational numbers like √105, aren't merely academic exercises. They have practical applications across various fields:
1. Geometry and Trigonometry
Square roots are fundamental in geometry. Calculations involving distances, areas, and volumes often require the use of the Pythagorean theorem (a² + b² = c²), which inherently involves square roots. Consider calculating the diagonal of a rectangle with sides of length 7 and 8 units. The diagonal length would involve calculating √(7² + 8²) = √113. Similar calculations are crucial in surveying, architecture, and engineering.
2. Physics and Engineering
Many physics formulas, especially those dealing with motion, energy, and forces, utilize square roots. For example, calculating the velocity of an object under gravitational acceleration involves the square root of various factors. In engineering, square roots appear in structural analysis, electrical circuit calculations, and other areas.
3. Computer Graphics and Game Development
Square roots are essential for vector calculations and distance computations in computer graphics and game development. Determining distances between points, normalizing vectors, and calculating the magnitude of vectors all rely heavily on square root calculations.
4. Statistics and Probability
Calculating standard deviations and variances in statistical analysis invariably involves the square root of sums of squared differences. These calculations are crucial for understanding data distributions and making statistical inferences.
5. Financial Modeling
In finance, square roots are frequently used in financial modeling, particularly in the context of option pricing models and risk management. Calculations involving volatility and portfolio optimization often necessitate the use of square roots.
Beyond the Square Root of 105: Expanding Our Understanding
While the specific numerical value of √105 is useful in certain contexts, the broader importance lies in grasping the concepts of square roots, irrational numbers, and numerical approximation techniques. These concepts form the bedrock of more advanced mathematical topics such as calculus, linear algebra, and numerical analysis. Understanding these methods allows us to approach complex mathematical problems with confidence and a deeper appreciation for the underlying principles.
Conclusion: The Value of Understanding
The seemingly simple question of "What is the square root of 105?" leads to a rich and rewarding exploration of mathematical concepts. From the simplicity of using a calculator to the elegance of the Babylonian method, various approaches highlight the multifaceted nature of numerical computation. The practical applications across diverse fields underscore the importance of this fundamental mathematical operation, making it a crucial element of both theoretical understanding and practical problem-solving. The quest for the numerical value serves as a launching pad to explore the beauty and power of mathematics.
Latest Posts
Latest Posts
-
What Percent Of 18 Is 27
Apr 03, 2025
-
How Many Ounces Are In A 1 4 Pound
Apr 03, 2025
-
What Percent Is 13 Of 16
Apr 03, 2025
-
What Is The Charge On A Potassium Ion
Apr 03, 2025
-
What Is The Symbol For Entropy
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
