What Is The Simplest Form Of 4 12
listenit
Mar 28, 2025 · 6 min read
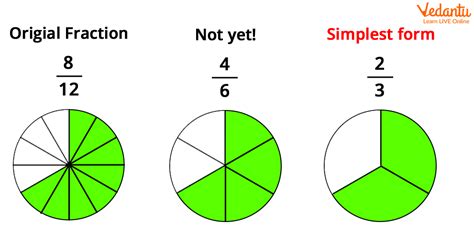
Table of Contents
What is the Simplest Form of 4/12? A Deep Dive into Fraction Simplification
The question, "What is the simplest form of 4/12?" might seem trivial at first glance. However, understanding how to simplify fractions is fundamental to mathematics and has far-reaching implications in various fields. This article delves into the process of simplifying fractions, explaining the concept in detail, providing multiple examples, and exploring its practical applications. We'll go beyond simply finding the answer to 4/12 and unpack the underlying principles to equip you with a robust understanding of fraction simplification.
Understanding Fractions
Before we tackle the simplification of 4/12, let's establish a firm grasp on what fractions represent. A fraction is a numerical representation of a part of a whole. It consists of two main components:
- Numerator: The top number in a fraction, indicating the number of parts we're considering.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 4/12, 4 is the numerator and 12 is the denominator. This means we're considering 4 parts out of a total of 12 equal parts.
Simplifying Fractions: The Concept of Equivalent Fractions
Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This doesn't change the value of the fraction; it merely represents it in a more concise and manageable form. Simplifying fractions relies on the concept of equivalent fractions. Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators.
For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half. The process of simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Finding the Greatest Common Divisor (GCD)
The GCD, also known as the greatest common factor (GCF), is the largest number that divides both the numerator and the denominator without leaving a remainder. There are several methods to find the GCD:
1. Listing Factors: This method involves listing all the factors of both the numerator and the denominator and identifying the largest factor they share. For example, let's find the GCD of 4 and 12:
- Factors of 4: 1, 2, 4
- Factors of 12: 1, 2, 3, 4, 6, 12
The largest common factor is 4.
2. Prime Factorization: This method involves expressing both the numerator and denominator as a product of their prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The common prime factor is 2², so the GCD is 4.
3. Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to find the GCD of 4 and 12:
- 12 ÷ 4 = 3 with a remainder of 0.
Since the remainder is 0, the GCD is the divisor, which is 4.
Simplifying 4/12
Now, let's apply our knowledge to simplify 4/12. We've already determined that the GCD of 4 and 12 is 4. To simplify the fraction, we divide both the numerator and the denominator by the GCD:
4/12 = (4 ÷ 4) / (12 ÷ 4) = 1/3
Therefore, the simplest form of 4/12 is 1/3.
Practical Applications of Fraction Simplification
Simplifying fractions is not just an academic exercise; it has numerous real-world applications:
- Cooking and Baking: Recipes often involve fractions, and simplifying them makes it easier to measure ingredients accurately.
- Construction and Engineering: Precise measurements are critical, and simplified fractions improve accuracy and reduce errors.
- Finance and Accounting: Calculations involving percentages and proportions often involve fractions, and simplification enhances clarity and efficiency.
- Data Analysis: Simplifying fractions helps in representing data concisely and understanding proportions more easily.
- Everyday Life: Numerous situations, from dividing resources to understanding proportions, require working with fractions, and simplifying them makes the process easier.
Beyond 4/12: More Examples of Fraction Simplification
Let's explore a few more examples to solidify our understanding:
Example 1: Simplify 6/18
- Find the GCD of 6 and 18. The GCD is 6.
- Divide both the numerator and denominator by 6: (6 ÷ 6) / (18 ÷ 6) = 1/3
The simplest form of 6/18 is 1/3.
Example 2: Simplify 15/25
- Find the GCD of 15 and 25. The GCD is 5.
- Divide both the numerator and denominator by 5: (15 ÷ 5) / (25 ÷ 5) = 3/5
The simplest form of 15/25 is 3/5.
Example 3: Simplify 24/36
- Find the GCD of 24 and 36. The GCD is 12.
- Divide both the numerator and denominator by 12: (24 ÷ 12) / (36 ÷ 12) = 2/3
The simplest form of 24/36 is 2/3.
Example 4: Simplify 10/100
- Find the GCD of 10 and 100. The GCD is 10.
- Divide both the numerator and denominator by 10: (10 ÷ 10) / (100 ÷ 10) = 1/10
The simplest form of 10/100 is 1/10.
Example 5 (dealing with larger numbers): Simplify 144/216
- Find the GCD of 144 and 216. Using prime factorization: 144 = 2⁴ x 3² and 216 = 2³ x 3³. The GCD is 2³ x 3² = 72.
- Divide both the numerator and denominator by 72: (144 ÷ 72) / (216 ÷ 72) = 2/3
The simplest form of 144/216 is 2/3.
Improper Fractions and Mixed Numbers
While the examples above dealt with proper fractions (where the numerator is smaller than the denominator), we can also simplify improper fractions (where the numerator is greater than or equal to the denominator). Improper fractions can be converted into mixed numbers (a combination of a whole number and a proper fraction).
For example, let's simplify 16/4:
- The GCD of 16 and 4 is 4.
- Divide both by 4: (16 ÷ 4) / (4 ÷ 4) = 4/1 = 4
This improper fraction simplifies to the whole number 4.
Another example: simplify 14/3
- Divide 14 by 3: 14 ÷ 3 = 4 with a remainder of 2.
- This means 14/3 is equal to 4 and 2/3. This is a mixed number.
Conclusion
Simplifying fractions is a fundamental skill with broad applications. By understanding the concept of equivalent fractions and the process of finding the greatest common divisor, you can efficiently reduce fractions to their simplest forms. This skill improves accuracy in calculations and enhances comprehension in various fields. Remember the steps: find the GCD, then divide both the numerator and denominator by the GCD. Practice makes perfect – the more you practice, the faster and more accurately you'll be able to simplify fractions. The seemingly simple question, "What is the simplest form of 4/12?" opens the door to a deeper understanding of a crucial mathematical concept with significant real-world relevance.
Latest Posts
Latest Posts
-
In Which Layer Does Weather Occur
Mar 31, 2025
-
What Is The Opposite Of 9
Mar 31, 2025
-
How Many Neutrons Does Carbon 13 Have
Mar 31, 2025
-
How Do You Find The Mass Of A Cube
Mar 31, 2025
-
What Color Of Light Has The Highest Energy
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Simplest Form Of 4 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
