What Is The Negative Square Root Of 64
listenit
Apr 04, 2025 · 5 min read
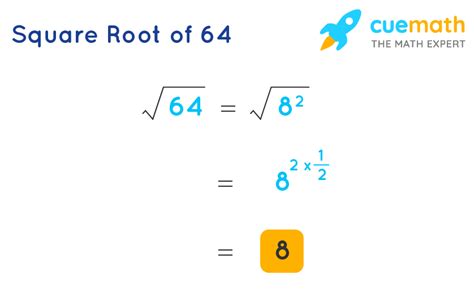
Table of Contents
What is the Negative Square Root of 64? Understanding Square Roots and Their Implications
The question, "What is the negative square root of 64?" might seem simple at first glance, but it delves into fundamental concepts within mathematics, particularly concerning square roots and their properties. Understanding this seemingly basic query opens doors to a wider appreciation of algebra and its applications. Let's explore this concept thoroughly.
Understanding Square Roots
Before diving into the negative square root of 64, it's crucial to grasp the core meaning of a square root. The square root of a number is a value that, when multiplied by itself (squared), results in the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This is often referred to as the principal square root.
However, the concept extends beyond this. Consider the equation x² = 9. While 3 is a solution (3 x 3 = 9), another solution exists: -3. (-3 x -3 = 9). This highlights the existence of two square roots for any positive number: one positive and one negative.
The Principal Square Root and its Notation
Mathematical notation typically prioritizes the principal square root, which is the non-negative square root. This convention helps avoid ambiguity in calculations and formulas. Therefore, √9 = 3, not -3. The symbol √ specifically denotes the principal square root.
Finding the Square Roots of 64
Now let's apply this understanding to the number 64. We need to find a number that, when multiplied by itself, equals 64. Through simple arithmetic or using a calculator, we quickly find that 8 x 8 = 64. Therefore, the principal square root of 64 is 8, written as √64 = 8.
However, as discussed earlier, there's another number that satisfies the condition: -8. Because (-8) x (-8) = 64, -8 is also a square root of 64.
Answering the Question: The Negative Square Root of 64
The question specifically asks for the negative square root of 64. Given our understanding, the answer is unequivocally -8. This is because (-8)² = 64.
Delving Deeper: Quadratic Equations and Solutions
The concept of square roots is intrinsically linked to solving quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants. These equations often have two solutions, which can be both real numbers, complex numbers (involving imaginary units), or sometimes even a single repeated root. Finding the square roots is often a crucial step in solving such equations. The quadratic formula, a powerful tool for solving quadratic equations, explicitly highlights the existence of these two potential solutions.
The Importance of Understanding Both Positive and Negative Roots
While the principal square root is convenient for many applications, neglecting the negative square root can lead to incomplete solutions or an incomplete understanding of the problem. Many mathematical and scientific problems require considering all possible solutions, including both positive and negative square roots. Ignoring the negative root can result in overlooking important physical phenomena or mathematical relationships. For instance, in physics, problems involving velocity often have two solutions, one positive (forward movement) and one negative (backward movement).
Applications in Various Fields
The concept of square roots, including negative ones, extends far beyond basic mathematics. They have crucial applications in various fields including:
1. Physics:
- Calculating velocities and accelerations: As mentioned earlier, solving kinematic equations often reveals both positive and negative solutions, each representing a different direction or physical interpretation.
- Quantum mechanics: Square roots are fundamental in calculations involving wave functions and probabilities.
- Calculating distances and magnitudes: In vector calculations, square roots are essential for determining magnitudes.
2. Engineering:
- Structural design: Calculations involving stress, strain, and stability frequently utilize square roots.
- Electrical engineering: AC circuit analysis utilizes complex numbers, which inherently involve square roots of negative numbers (imaginary units).
- Civil engineering: The calculation of areas and volumes often involves square roots.
3. Computer Science:
- Algorithm design: Square roots play a role in the efficiency of certain algorithms and data structures.
- Graphics and game development: Square roots are employed in calculating distances and performing transformations in 2D and 3D graphics.
- Cryptography: Complex mathematical computations involving square roots are involved in various cryptographic algorithms.
4. Finance:
- Compound interest calculations: Understanding the power of compounding involves working with exponents and roots.
- Investment analysis: Various financial models utilize square roots and other mathematical operations for risk assessment and portfolio management.
Complex Numbers and the Square Root of Negative Numbers
When dealing with the square roots of negative numbers, we enter the realm of complex numbers. These numbers extend the concept of real numbers by introducing the imaginary unit "i," defined as the square root of -1 (i² = -1). The negative square root of 64 can be expressed in terms of complex numbers although it's simply -8 in the context of real numbers. The idea of complex numbers is essential in higher-level mathematics, physics, and engineering, enabling solutions to equations that wouldn't otherwise be solvable using only real numbers.
Conclusion: The Significance of Mathematical Precision
The seemingly simple question, "What is the negative square root of 64?" underscores the importance of understanding the nuances of mathematical concepts. Knowing that the answer is -8 requires a solid grasp of square roots, their properties, and the existence of both positive and negative solutions. This understanding is pivotal for tackling more complex mathematical problems across various disciplines. Failing to appreciate the subtle differences between principal square roots and the broader concept of square roots can lead to errors and incomplete solutions. Therefore, precision and a thorough understanding of the underlying mathematical principles are essential for accurate and meaningful results. The exploration of this seemingly simple question offers a valuable lesson in the depth and breadth of mathematical concepts, highlighting their crucial role in the real world.
Latest Posts
Latest Posts
-
How Many Electrons Are In Titanium
Apr 04, 2025
-
Two Thirds Of A Number Algebraic Expression
Apr 04, 2025
-
Is Photosynthesis A Chemical Or Physical Change
Apr 04, 2025
-
Convert 101 Degrees Fahrenheit To Celsius
Apr 04, 2025
-
How Many Minute In A Week
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Negative Square Root Of 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
