What Is The Negative Square Root Of 4
listenit
Mar 31, 2025 · 5 min read
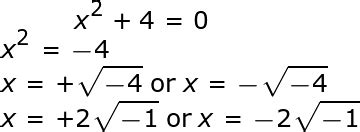
Table of Contents
What is the Negative Square Root of 4? Unraveling the Mysteries of Negative Roots
The question, "What is the negative square root of 4?" seems deceptively simple. However, delving into this seemingly straightforward mathematical concept reveals a rich tapestry of number systems, mathematical properties, and practical applications. This comprehensive guide will not only answer the question directly but also explore the underlying principles and broader implications within the realms of algebra and beyond.
Understanding Square Roots
Before we tackle the negative square root of 4, let's solidify our understanding of square roots in general. The square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 (√9) is 3 because 3 * 3 = 9. This is often referred to as the principal square root, which is always non-negative.
Principal Square Root vs. Other Roots
It's crucial to distinguish between the principal square root and other roots. While √9 = 3, there's another number that, when squared, yields 9: -3. (-3 * -3 = 9). However, the principal square root notation (√) always denotes the non-negative root. To represent both the positive and negative roots, we use the ± symbol. Therefore, the complete solution to x² = 9 is x = ±√9 = ±3.
The Negative Square Root of 4: The Solution
Now, let's address the specific question: What is the negative square root of 4?
The square root of 4 (√4) is 2, because 2 * 2 = 4. However, the question asks for the negative square root. This means we're looking for a number that, when multiplied by itself, equals 4, and that number is negative. That number is -2. This is because (-2) * (-2) = 4.
Therefore, the negative square root of 4 is -2.
Expanding into Complex Numbers
While real numbers adequately address the negative square root of 4, the concept extends further into the realm of complex numbers when dealing with negative radicands (the number inside the square root symbol).
Let's consider the square root of -4 (√-4). There's no real number that, when multiplied by itself, results in a negative number. This is where imaginary numbers come into play. The imaginary unit, denoted as 'i', is defined as the square root of -1 (√-1 = i).
Using this definition, we can rewrite √-4 as follows:
√-4 = √(4 * -1) = √4 * √-1 = 2i
This means the square root of -4 is 2i. It's an imaginary number, not a real number. The concept of negative square roots becomes significantly richer when we introduce complex numbers, which are numbers that consist of both real and imaginary parts (a + bi, where 'a' and 'b' are real numbers).
Applications of Square Roots and Complex Numbers
The concepts of square roots and complex numbers, although seemingly abstract, find extensive practical applications in various fields:
1. Physics and Engineering:
- AC Circuit Analysis: Complex numbers are crucial for analyzing alternating current (AC) circuits. Impedance, a measure of opposition to current flow, is often represented as a complex number.
- Quantum Mechanics: Complex numbers are fundamental to quantum mechanics, which describes the behavior of matter at the atomic and subatomic levels. Wave functions, which describe the state of a quantum system, are often complex-valued.
- Signal Processing: Complex numbers are used extensively in signal processing to analyze and manipulate signals. The Fourier transform, a fundamental tool in signal processing, uses complex numbers.
2. Mathematics:
- Solving Quadratic Equations: The quadratic formula, a powerful tool for solving quadratic equations (ax² + bx + c = 0), frequently involves square roots and may yield complex roots.
- Geometry: Square roots are fundamental to calculations involving distances, areas, and volumes in geometry. For example, the Pythagorean theorem (a² + b² = c²) uses square roots to determine the length of the hypotenuse of a right-angled triangle.
3. Computer Science:
- Computer Graphics: Complex numbers and square roots are used in computer graphics for transformations, rotations, and scaling of images.
- Cryptography: Complex numbers play a role in cryptographic algorithms, contributing to secure communication and data protection.
Solving Problems Involving Negative Square Roots
Let's delve into some example problems that illustrate the application of negative square roots:
Problem 1: Solve the equation x² = 16.
Solution: The solutions are x = ±√16 = ±4. This means x can be either 4 or -4.
Problem 2: Find the roots of the quadratic equation x² + 2x + 5 = 0.
Solution: Using the quadratic formula, we get:
x = [-b ± √(b² - 4ac)] / 2a
In this case, a = 1, b = 2, and c = 5. Substituting these values yields:
x = [-2 ± √(4 - 20)] / 2 = [-2 ± √(-16)] / 2 = [-2 ± 4i] / 2 = -1 ± 2i
The roots are complex numbers: -1 + 2i and -1 - 2i.
Problem 3: Simplify √(-9) * √(-25)
Solution: We can rewrite this as:
√(-9) * √(-25) = (√9 * √-1) * (√25 * √-1) = (3i) * (5i) = 15i² = -15.
Beyond the Basics: Higher Order Roots
The concept of square roots extends to higher-order roots, such as cube roots (∛), fourth roots (∜), and so on. For example, the cube root of 8 (∛8) is 2, because 2 * 2 * 2 = 8. However, cube roots of negative numbers are also real numbers, unlike square roots. For instance, ∛-8 = -2, because (-2) * (-2) * (-2) = -8.
Conclusion
The seemingly simple question, "What is the negative square root of 4?" opens doors to a deeper understanding of number systems, mathematical operations, and their wide-ranging applications. From the real numbers to the realm of complex numbers, the concept expands beyond simple arithmetic, revealing its significance in diverse fields, including physics, engineering, mathematics, and computer science. Mastering the concepts of square roots and complex numbers is crucial for anyone pursuing studies or careers in these areas. This exploration solidifies the idea that even fundamental mathematical questions can lead to fascinating discoveries and intricate applications. The journey from understanding the negative square root of 4 to grasping the complexities of complex numbers highlights the beauty and power of mathematics.
Latest Posts
Latest Posts
-
How Many Neutrons Does Molybdenum Have
Apr 02, 2025
-
How Monomers Are Related To Polymers
Apr 02, 2025
-
Does Gas Take The Shape Of Its Container
Apr 02, 2025
-
2 5 To The Power Of 3
Apr 02, 2025
-
How Are Chemical Bonds Important To Metabolism
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Negative Square Root Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
