What Is The Lcm Of 8 10
listenit
Mar 28, 2025 · 4 min read
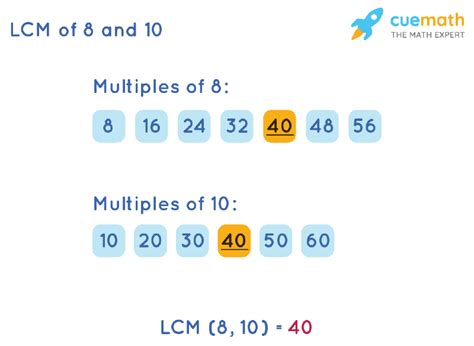
Table of Contents
What is the LCM of 8 and 10? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with wide-ranging applications in various fields. This article will thoroughly explore how to calculate the LCM of 8 and 10, explain the underlying principles, and demonstrate different methods for finding the LCM of any two numbers. We'll also delve into the practical uses of LCMs and address common misconceptions.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 8 and 10, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) of the original numbers can divide into evenly.
Example: Consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 8 and 10: Three Methods
There are several ways to calculate the LCM of 8 and 10. We'll explore three common methods:
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
The smallest number appearing in both lists is 40. Therefore, the LCM of 8 and 10 is 40.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 10: 2 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2³ = 8
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 8 x 5 = 40. Therefore, the LCM of 8 and 10 is 40.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are intimately related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers.
First, we need to find the greatest common divisor (GCD) of 8 and 10. The GCD is the largest number that divides both 8 and 10 without leaving a remainder. The GCD of 8 and 10 is 2.
Now, we can use the formula:
LCM(8, 10) * GCD(8, 10) = 8 * 10 LCM(8, 10) * 2 = 80 LCM(8, 10) = 80 / 2 LCM(8, 10) = 40
Therefore, the LCM of 8 and 10 is 40.
Applications of Least Common Multiples
The concept of LCM has practical applications in various areas, including:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One arrives every 8 minutes, and the other every 10 minutes. The LCM (40 minutes) determines when both buses will arrive at the stop simultaneously.
-
Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, adding 1/8 and 1/10 requires finding the LCM of 8 and 10 (which is 40), converting the fractions to equivalent fractions with a denominator of 40, and then adding them.
-
Geometry: LCM is used in solving problems related to tiling and patterns where repetitive elements are involved.
-
Music: In music theory, the LCM helps determine the least common multiple of note durations to find when two musical phrases will align rhythmically.
-
Computer Science: The concept of LCM has applications in algorithms and data structures, especially in problems involving synchronization and cyclical events.
Common Misconceptions about LCM
-
LCM is always larger than the larger number: While this is often true, it's not always the case. If one number is a multiple of the other, the LCM will be equal to the larger number. For example, the LCM of 4 and 8 is 8.
-
LCM is only applicable to two numbers: The LCM can be calculated for any number of integers. The process involves extending the methods described earlier to encompass multiple numbers.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a valuable skill with practical applications in various fields. Understanding the different methods for calculating the LCM, including listing multiples, prime factorization, and utilizing the GCD relationship, empowers you to efficiently solve problems involving LCMs. By mastering these techniques, you'll not only enhance your mathematical understanding but also gain a practical tool applicable to a wide range of real-world scenarios. Remember to choose the method that best suits the numbers involved for optimal efficiency. For smaller numbers, listing multiples might suffice, while prime factorization proves more efficient for larger numbers. The formula relating LCM and GCD provides an elegant and powerful alternative for various applications. The LCM of 8 and 10, definitively 40, serves as a clear and concise example to illustrate these methods.
Latest Posts
Latest Posts
-
What Is 5 5 As A Decimal
Mar 31, 2025
-
Is Gasoline Evaporating A Chemical Change
Mar 31, 2025
-
What Is Half Of A Mile In Feet
Mar 31, 2025
-
Common Factors Of 20 And 36
Mar 31, 2025
-
Simplify The Square Root Of 288
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
