What Is The Lcm Of 5 And 6
listenit
Apr 05, 2025 · 4 min read
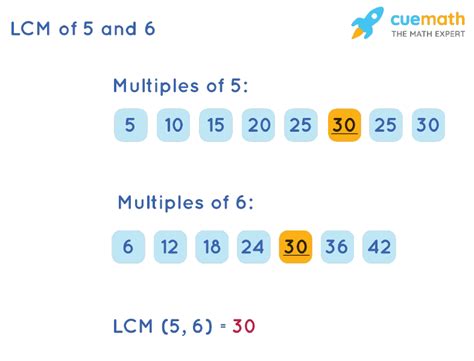
Table of Contents
What is the LCM of 5 and 6? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex algebraic problems. This article will delve into the process of determining the LCM of 5 and 6, explaining different methods and providing a deeper understanding of the underlying principles. We'll also explore the broader context of LCMs and their significance in various mathematical fields.
Understanding Least Common Multiples (LCM)
Before we tackle the specific case of 5 and 6, let's establish a solid foundation in understanding LCMs. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive whole number.
- Multiple of All Numbers: It's divisible by each of the given numbers without leaving a remainder.
- Smallest Possible Value: It's the smallest number that satisfies the above condition.
Methods for Finding the LCM of 5 and 6
There are several effective ways to calculate the LCM of 5 and 6. We'll explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
Multiples of 6: 6, 12, 18, 24, 30, 36...
Notice that the smallest number appearing in both lists is 30. Therefore, the LCM of 5 and 6 is 30.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves expressing each number as a product of its prime factors.
- Prime Factorization of 5: 5 (5 is a prime number)
- Prime Factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiply these highest powers together: 2 x 3 x 5 = 30
Therefore, the LCM of 5 and 6 using prime factorization is 30.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 5 and 6 using the Euclidean algorithm:
- Divide the larger number (6) by the smaller number (5): 6 ÷ 5 = 1 with a remainder of 1.
- Replace the larger number with the smaller number (5) and the smaller number with the remainder (1): 5 ÷ 1 = 5 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 1. GCD(5, 6) = 1
Now, we can use the formula:
LCM(5, 6) x GCD(5, 6) = 5 x 6 LCM(5, 6) x 1 = 30 LCM(5, 6) = 30
This method demonstrates the interconnectedness of LCM and GCD.
Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various fields:
1. Fraction Operations
LCM is essential when adding or subtracting fractions with different denominators. To add fractions, we need a common denominator, and the LCM provides the smallest such denominator, simplifying calculations. For example:
1/5 + 1/6 = (6/30) + (5/30) = 11/30
2. Scheduling and Timing Problems
LCM is frequently used in scheduling problems. For example, if two buses depart from a station at different intervals, the LCM of these intervals determines when they will depart simultaneously again.
3. Cyclic Patterns and Repeating Events
LCM can be applied to problems involving repeating events or cyclic patterns. For instance, if two events occur at regular intervals, the LCM of their intervals indicates when both events will coincide.
4. Number Theory and Abstract Algebra
LCM is a fundamental concept in number theory, forming the basis for advanced mathematical concepts like modular arithmetic and ring theory.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we consider all prime factors of all the numbers and take the highest power of each. For the listing multiples method, we list the multiples of all numbers until we find the smallest common multiple.
Conclusion: The Significance of Understanding LCM
The LCM of 5 and 6, calculated to be 30 using various methods, serves as a simple yet illustrative example of a fundamental mathematical concept. Understanding LCM is crucial not only for solving mathematical problems but also for tackling real-world applications across diverse fields. Mastering different methods for calculating LCM empowers you to approach a wider range of problems efficiently and confidently. The understanding of LCM extends beyond simple calculations, forming a cornerstone in more advanced mathematical concepts and practical problem-solving scenarios. The interconnectedness between LCM and GCD further highlights the rich and interwoven nature of mathematical relationships. By thoroughly grasping this concept, you're equipping yourself with a valuable tool for various mathematical and practical endeavors.
Latest Posts
Latest Posts
-
Write The Formula Formula Unit For The Following Compounds
Apr 06, 2025
-
21 Is 42 Of What Number
Apr 06, 2025
-
Initial Value And Rate Of Change
Apr 06, 2025
-
500 Ml Equals How Many Oz
Apr 06, 2025
-
I Have But One Life To Give
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
