Initial Value And Rate Of Change
listenit
Apr 06, 2025 · 6 min read
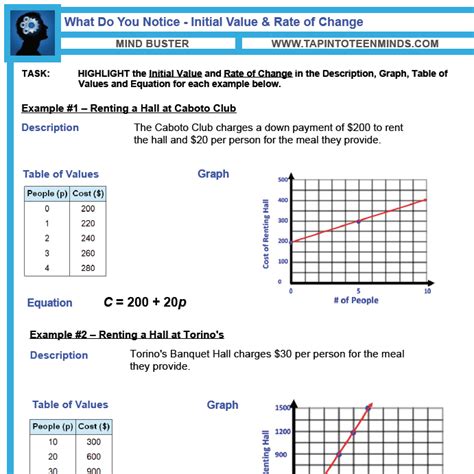
Table of Contents
Initial Value and Rate of Change: Understanding the Fundamentals of Growth and Decay
Understanding the concepts of initial value and rate of change is crucial in various fields, from simple arithmetic to complex calculus and real-world applications like finance, physics, and biology. These two concepts form the backbone of understanding growth and decay models, allowing us to predict future values based on past trends. This article will delve deep into these concepts, explaining their meaning, how they relate to each other, and how they're applied in different contexts.
What is Initial Value?
The initial value, also known as the starting value, base value, or y-intercept, represents the value of a quantity at the beginning of a process or time period (t=0). It's the foundation upon which subsequent changes are built. Imagine you're tracking the growth of a plant. The initial value would be the plant's height when you first started observing it. Similarly, in finance, the initial value might represent the principal amount of an investment or loan.
Examples of Initial Value:
- Population Growth: The initial population of a city at the start of a study.
- Investment Growth: The principal amount invested in a savings account.
- Radioactive Decay: The initial amount of a radioactive substance.
- Cooling of an Object: The initial temperature of an object before it begins to cool.
- Free Fall: The initial height of an object before it falls.
In mathematical terms, the initial value is often represented by the variable a in equations like: y = a * b^x (exponential growth/decay) or y = mx + a (linear function).
What is Rate of Change?
The rate of change describes how a quantity changes over time or in relation to another variable. It quantifies the speed or intensity of the change. A positive rate of change indicates growth or increase, while a negative rate of change signifies decay or decrease. The rate of change is also crucial in determining the slope of a line or the tangent to a curve.
Types of Rate of Change:
-
Average Rate of Change: This is the overall change over a specific interval. It's calculated by finding the difference between the final and initial values and dividing by the change in the independent variable (usually time). Formula:
(y2 - y1) / (x2 - x1). -
Instantaneous Rate of Change: This refers to the rate of change at a single point in time. In calculus, this is found by calculating the derivative of the function at that point.
Examples of Rate of Change:
- Speed: The rate of change of distance with respect to time.
- Acceleration: The rate of change of velocity with respect to time.
- Population Growth Rate: The rate at which a population increases or decreases per unit of time (e.g., per year).
- Interest Rate: The rate at which an investment earns interest.
- Rate of Cooling: How quickly an object loses heat.
The Relationship Between Initial Value and Rate of Change
The initial value and rate of change are interconnected and essential for understanding the behavior of a quantity over time. The initial value provides the starting point, while the rate of change determines the trajectory of the quantity. Together, they completely define a linear function and are crucial components of many other models.
Linear Growth and Decay
In linear growth or decay models, the rate of change is constant. The equation is often expressed as:
y = mx + a
where:
yis the dependent variable (the value we're tracking)mis the rate of change (slope of the line)xis the independent variable (usually time)ais the initial value (y-intercept)
A positive m indicates linear growth, while a negative m indicates linear decay.
Exponential Growth and Decay
Exponential growth and decay models represent situations where the rate of change is proportional to the current value. This leads to a much faster increase or decrease than linear models. The general equation is:
y = a * b^x
where:
yis the dependent variableais the initial valuebis the growth/decay factor (1 + rate of change for growth, 1 - rate of change for decay)xis the independent variable (usually time)
If b > 1, it represents exponential growth; if 0 < b < 1, it represents exponential decay.
Real-World Applications
Understanding initial value and rate of change is crucial for numerous real-world applications:
1. Finance:
- Compound Interest: Calculating the future value of an investment involves using the initial value (principal amount), the interest rate (rate of change), and the time period.
- Loan Amortization: Determining monthly payments on a loan requires understanding the initial loan amount, interest rate, and loan term.
2. Physics:
- Motion: Calculating the position, velocity, and acceleration of an object involves understanding the initial position (initial value), velocity (initial rate of change), and acceleration (rate of change of velocity).
- Radioactive Decay: The initial amount of a radioactive substance and its half-life (related to the rate of decay) allow scientists to predict how much of the substance will remain after a certain time.
3. Biology:
- Population Dynamics: Modeling population growth or decline requires understanding the initial population size and the birth and death rates (rates of change).
- Bacterial Growth: The growth of bacteria follows an exponential model, where the initial number of bacteria and the growth rate determine the future population size.
4. Economics:
- Economic Growth: Measuring a country's economic growth involves understanding the initial GDP and the rate of economic growth.
- Inflation: Tracking inflation involves understanding the initial price level and the rate of inflation (rate of change of prices).
5. Environmental Science:
- Pollution Levels: Monitoring pollution levels requires understanding the initial pollution level and the rate at which it increases or decreases.
- Climate Change: Modeling climate change involves understanding the initial temperature and the rate at which it is changing.
Analyzing Data to Determine Initial Value and Rate of Change
Determining the initial value and rate of change from data often involves graphical analysis and/or calculations.
Graphical Analysis:
- Linear Relationships: For linear relationships, the initial value is the y-intercept (where the line crosses the y-axis), and the rate of change is the slope of the line (rise over run).
- Exponential Relationships: For exponential relationships, the initial value is the y-intercept, and the rate of change can be determined by observing how quickly the curve increases or decreases.
Calculations:
- Linear Relationships: Using two data points (x1, y1) and (x2, y2), the rate of change (slope) can be calculated using the formula:
(y2 - y1) / (x2 - x1). The initial value can be found by substituting one of the data points into the equationy = mx + aand solving fora. - Exponential Relationships: More sophisticated methods, often involving logarithmic transformations or curve fitting techniques, are needed to determine the initial value and rate of change from exponential data.
Conclusion
Initial value and rate of change are fundamental concepts with widespread applications across diverse fields. Understanding these concepts provides the tools to model growth and decay processes, make predictions about future trends, and analyze data effectively. Whether you're analyzing financial investments, studying population dynamics, or modeling physical phenomena, a solid grasp of initial value and rate of change is indispensable. By mastering these concepts, you can gain deeper insights into the world around you and make more informed decisions. Further exploration into calculus and statistical analysis will significantly enhance your ability to work with these concepts in increasingly complex situations.
Latest Posts
Latest Posts
-
Which Quadrilaterals Always Have Diagonals That Are Congruent
Apr 07, 2025
-
Elements In Groups 3 Through 12 Are Called
Apr 07, 2025
-
Only One Pair Of Parallel Sides
Apr 07, 2025
-
How Many Ounces Is Two Pints
Apr 07, 2025
-
Combination Of Chemical Symbols And Numbers To Represent A Substance
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Initial Value And Rate Of Change . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.