What Is The Fraction Of 0.85
listenit
Apr 01, 2025 · 5 min read
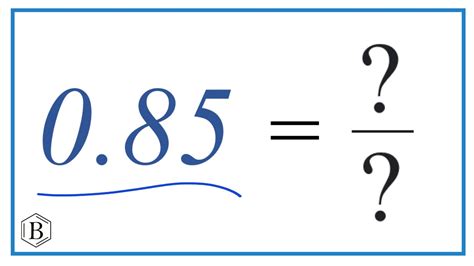
Table of Contents
What is the Fraction of 0.85? A Deep Dive into Decimal-to-Fraction Conversion
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This seemingly simple task holds significant importance in various fields, from basic arithmetic to advanced calculus. This comprehensive guide will explore the conversion of the decimal 0.85 into a fraction, offering a step-by-step process, tackling common misconceptions, and providing insightful examples to solidify your understanding. We'll also delve into the broader context of decimal-to-fraction conversion, equipping you with the skills to handle any similar problem.
Understanding Decimals and Fractions
Before jumping into the conversion, let's briefly review the concepts of decimals and fractions.
Decimals: Decimals represent numbers that are not whole numbers. They utilize a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, in 0.85, the 8 represents 8 tenths and the 5 represents 5 hundredths.
Fractions: Fractions represent a part of a whole. They are expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, and the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Converting 0.85 to a Fraction: The Step-by-Step Process
The conversion of 0.85 to a fraction involves a straightforward process:
Step 1: Identify the Place Value of the Last Digit
In 0.85, the last digit (5) is in the hundredths place. This means that the decimal represents 85 hundredths.
Step 2: Write the Decimal as a Fraction
Based on Step 1, we can write 0.85 as a fraction: 85/100. This is our initial, unsimplified fraction.
Step 3: Simplify the Fraction
The fraction 85/100 can be simplified by finding the greatest common divisor (GCD) of the numerator (85) and the denominator (100). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Finding the GCD can be done through several methods:
-
Listing Factors: List the factors of both 85 and 100 and identify the largest common factor. Factors of 85 are 1, 5, 17, and 85. Factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100. The greatest common factor is 5.
-
Prime Factorization: Express both numbers as a product of their prime factors. 85 = 5 x 17 and 100 = 2 x 2 x 5 x 5. The common prime factor is 5.
Once the GCD (5) is found, divide both the numerator and the denominator by it:
85 ÷ 5 = 17 100 ÷ 5 = 20
Therefore, the simplified fraction is 17/20.
Understanding the Concept of Simplification
Simplifying fractions is crucial for several reasons:
-
Clarity: Simplified fractions are easier to understand and work with. 17/20 is much more intuitive than 85/100.
-
Standard Form: Presenting fractions in their simplest form is a mathematical convention.
-
Efficiency: Simplified fractions make calculations involving fractions more efficient.
Practical Applications and Real-World Examples
The ability to convert decimals to fractions is vital in numerous contexts:
-
Baking and Cooking: Recipes often call for fractional measurements of ingredients. Understanding decimal-to-fraction conversion ensures accurate measurements. For example, a recipe might require 0.85 cups of flour, which is equivalent to 17/20 cups.
-
Engineering and Construction: Precise measurements are paramount in these fields. Converting decimals to fractions allows for accurate calculations and precise construction.
-
Finance: Working with percentages and proportions often involves converting decimals to fractions for easier calculations. For example, calculating interest rates or determining proportions of investments often requires this skill.
-
Data Analysis: When analyzing data represented as decimals, converting them to fractions can provide a clearer understanding of the relationships between different parts of the data.
Beyond 0.85: Converting Other Decimals to Fractions
The method used for converting 0.85 to a fraction applies to other decimals as well. Let's consider some additional examples:
Example 1: Converting 0.75 to a fraction
- The last digit is in the hundredths place, so the decimal can be written as 75/100.
- The GCD of 75 and 100 is 25.
- Dividing both numerator and denominator by 25 gives us 3/4.
Therefore, 0.75 = 3/4.
Example 2: Converting 0.6 to a fraction
- The last digit is in the tenths place, so the decimal can be written as 6/10.
- The GCD of 6 and 10 is 2.
- Dividing both numerator and denominator by 2 gives us 3/5.
Therefore, 0.6 = 3/5.
Example 3: Converting 0.125 to a fraction
- The last digit is in the thousandths place, so the decimal can be written as 125/1000.
- The GCD of 125 and 1000 is 125.
- Dividing both numerator and denominator by 125 gives us 1/8.
Therefore, 0.125 = 1/8.
Dealing with Repeating Decimals
Converting repeating decimals to fractions is slightly more complex and requires a different approach. Repeating decimals, such as 0.333... (0.3 recurring), cannot be directly converted using the method described above. Specialized techniques involving algebraic manipulation are necessary for such conversions.
Conclusion: Mastering Decimal-to-Fraction Conversion
Converting decimals to fractions is a core mathematical skill with wide-ranging applications. This guide has provided a thorough explanation of the conversion process, focusing on the step-by-step methodology and highlighting the importance of simplification. By understanding the underlying principles and practicing with various examples, you'll develop proficiency in converting decimals to fractions, enhancing your mathematical abilities and problem-solving skills. Remember, practice is key to mastering this essential concept. Continue practicing different decimal conversions to solidify your understanding and build confidence in your mathematical abilities. The more you practice, the quicker and more accurate you'll become at this important skill.
Latest Posts
Latest Posts
-
How To Solve Multi Step Inequalities
Apr 02, 2025
-
Percent Composition Of Mg No3 2
Apr 02, 2025
-
How To Convert 3 8 Into A Decimal
Apr 02, 2025
-
Natural Resources Of The Northeast Region
Apr 02, 2025
-
How Many Unpaired Electrons Are In Sulfur
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction Of 0.85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
