What Is The Fraction For 0.85
listenit
Mar 28, 2025 · 5 min read
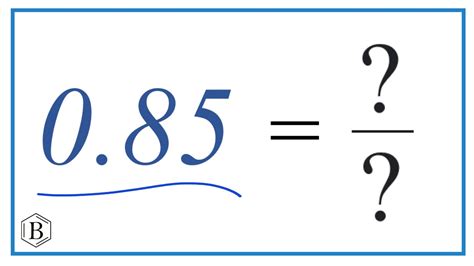
Table of Contents
What is the Fraction for 0.85? A Deep Dive into Decimal-to-Fraction Conversion
The question, "What is the fraction for 0.85?" seems simple at first glance. However, understanding the underlying process of converting decimals to fractions reveals a fundamental concept in mathematics with broader applications. This article will not only answer the question directly but also explore the method, variations, and practical implications of decimal-to-fraction conversion. We'll delve into the process, discuss simplifying fractions, and even touch upon the use of this conversion in different fields. By the end, you'll be confident in converting any decimal to its fractional equivalent.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions.
-
Decimals: Decimals represent parts of a whole using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.85 represents 8 tenths and 5 hundredths.
-
Fractions: Fractions represent parts of a whole using a numerator (top number) and a denominator (bottom number). The numerator indicates the number of parts, and the denominator indicates the total number of parts the whole is divided into. For instance, ½ represents one part out of two equal parts.
Converting 0.85 to a Fraction: The Step-by-Step Process
The conversion of 0.85 to a fraction involves these simple steps:
-
Write the decimal as a fraction with a denominator of 1: This is our starting point. We write 0.85 as 0.85/1.
-
Multiply both the numerator and denominator by a power of 10 to eliminate the decimal point: Since there are two digits after the decimal point, we multiply both the numerator and the denominator by 100 (10²). This moves the decimal point two places to the right. This gives us (0.85 x 100) / (1 x 100) = 85/100.
-
Simplify the fraction: This step involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD of 85 and 100 is 5. Dividing both the numerator and denominator by 5, we get: 85/100 = (85 ÷ 5) / (100 ÷ 5) = 17/20.
Therefore, the fraction for 0.85 is 17/20.
Why Simplifying Fractions is Important
Simplifying a fraction to its lowest terms is crucial for several reasons:
-
Clarity: A simplified fraction is easier to understand and interpret. 17/20 is more readily grasped than 85/100.
-
Comparability: Simplifying fractions makes it easier to compare them. For instance, comparing 17/20 to other fractions becomes simpler than comparing 85/100.
-
Calculations: Simplified fractions make calculations (addition, subtraction, multiplication, and division) easier and less prone to errors.
Variations and More Complex Decimal Conversions
While 0.85 is a relatively straightforward conversion, let's explore some variations:
-
Decimals with a single digit after the decimal point: For example, converting 0.7 to a fraction involves multiplying by 10 to get 7/10. This fraction is already in its simplest form.
-
Decimals with more than two digits after the decimal point: For instance, converting 0.125:
- 0.125/1
- (0.125 x 1000) / (1 x 1000) = 125/1000
- Simplifying by dividing by 125 (the GCD), we get 1/8.
-
Repeating decimals: Converting repeating decimals (like 0.333...) to fractions requires a slightly different approach. This involves setting up an equation and solving for the fraction. For example, to convert 0.333... to a fraction:
- Let x = 0.333...
- Multiply both sides by 10: 10x = 3.333...
- Subtract the first equation from the second: 10x - x = 3.333... - 0.333...
- This simplifies to 9x = 3
- Solving for x gives x = 3/9, which simplifies to 1/3.
-
Mixed decimals: A mixed decimal is a number that contains both a whole number and a decimal part (e.g., 2.75). You convert the decimal part to a fraction, then add it to the whole number. 2.75 converts to 2 and 75/100 or 2 and ¾ after simplification.
Applications of Decimal-to-Fraction Conversions
The ability to convert decimals to fractions is not merely an academic exercise. It has practical applications across various fields:
-
Cooking and Baking: Recipes often use fractional measurements (e.g., ½ cup, ¼ teaspoon). Converting decimal measurements from digital scales to fractional equivalents ensures accuracy.
-
Engineering and Construction: Precision is paramount in these fields. Converting decimal measurements to fractions can improve accuracy in blueprints and calculations.
-
Finance: Fractions are used to represent percentages and proportions in financial calculations, making decimal-to-fraction conversion essential for accurate accounting.
-
Data Analysis: When working with data, representing proportions as fractions can improve clarity and simplify calculations.
Advanced Concepts and Further Exploration
For those seeking to delve deeper into the world of fractions and decimals, consider exploring these advanced topics:
-
Continued Fractions: This is a way of representing a number as a sum of fractions where each fraction has a numerator of 1 and a denominator that is a whole number.
-
Rational and Irrational Numbers: Understanding the difference between rational numbers (numbers that can be expressed as a fraction) and irrational numbers (numbers that cannot be expressed as a fraction, such as π or √2) provides a broader mathematical perspective.
-
Approximations: Sometimes, it is more practical to use a close approximation of a decimal as a fraction. For instance, using 22/7 as an approximation for π in certain calculations is acceptable when high precision is not required.
Conclusion
Converting 0.85 to a fraction, as demonstrated, involves straightforward steps: writing it as 85/100, and then simplifying it to its lowest form, 17/20. This seemingly simple task reveals the fundamental relationship between decimals and fractions, highlighting the importance of understanding these core mathematical concepts. This process extends beyond simple conversions, finding application in various real-world scenarios where precision and clarity are essential. Mastering this conversion process enhances mathematical skills and provides a valuable tool for countless applications. By understanding the process, its variations, and its practical uses, you can confidently tackle any decimal-to-fraction conversion and further your mathematical proficiency.
Latest Posts
Latest Posts
-
The Least Common Multiple Of 6 And 9
Mar 31, 2025
-
6 1 2 As An Improper Fraction
Mar 31, 2025
-
How Do Sedimentary Rocks Change Into Igneous Rocks
Mar 31, 2025
-
The Sum Of 3 Consecutive Integers
Mar 31, 2025
-
Is Benzene A Pure Substance Or Mixture
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction For 0.85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
