What Is The Fraction For 0.04
listenit
Mar 31, 2025 · 5 min read
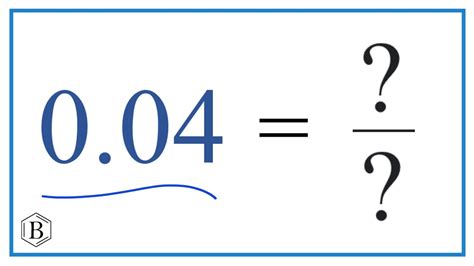
Table of Contents
What is the Fraction for 0.04? A Comprehensive Guide
Understanding decimal-to-fraction conversions is a fundamental skill in mathematics. This comprehensive guide will delve deep into the process of converting the decimal 0.04 into a fraction, exploring various methods, and providing a solid foundation for tackling similar conversions. We'll go beyond simply finding the answer and explore the underlying concepts, making this a valuable resource for students and anyone looking to brush up on their fraction skills.
Understanding Decimals and Fractions
Before we jump into converting 0.04, let's refresh our understanding of decimals and fractions.
-
Decimals: Decimals represent parts of a whole number using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.04 represents four hundredths.
-
Fractions: Fractions represent parts of a whole number as a ratio of two integers: a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered. For example, 1/4 represents one out of four equal parts.
The key to converting between decimals and fractions lies in understanding the place value of the digits in the decimal.
Method 1: Using Place Value to Convert 0.04 to a Fraction
The simplest way to convert 0.04 to a fraction is to directly interpret its place value.
The digit 4 is in the hundredths place. This means 0.04 represents 4 hundredths, which can be written as a fraction:
4/100
This fraction is already in a form that is easily understandable, but we can further simplify it.
Method 2: Simplifying the Fraction
The fraction 4/100 can be simplified by finding the greatest common divisor (GCD) of the numerator (4) and the denominator (100). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
The GCD of 4 and 100 is 4. We can divide both the numerator and the denominator by 4 to simplify the fraction:
4 ÷ 4 = 1 100 ÷ 4 = 25
Therefore, the simplified fraction is:
1/25
This is the simplest form of the fraction representing 0.04.
Method 3: Using the Power of Ten
Another approach involves understanding that decimals are essentially fractions with a denominator that is a power of ten.
0.04 can be written as:
4 × (1/100) or 4/100
This directly provides us with the initial fraction 4/100, which, as we've seen, simplifies to 1/25. This method highlights the inherent relationship between decimals and fractions with powers of ten as denominators.
Why Simplifying Fractions is Important
Simplifying fractions is crucial for several reasons:
-
Clarity: A simplified fraction is easier to understand and visualize. 1/25 is much clearer than 4/100.
-
Comparison: Simplified fractions make it easier to compare fractions. For example, it's easier to compare 1/25 to 1/10 than 4/100 to 10/100.
-
Calculations: Simplified fractions often lead to easier calculations in more complex mathematical operations.
Practical Applications of Decimal-to-Fraction Conversions
Converting decimals to fractions is a fundamental skill with widespread applications across various fields:
-
Baking and Cooking: Recipes often require precise measurements, where understanding fractions and decimals is essential.
-
Engineering and Construction: Accurate measurements and calculations in blueprints and designs heavily rely on fractions and decimals.
-
Finance: Understanding percentages and interest calculations requires a strong foundation in decimal-to-fraction conversions.
-
Data Analysis: In statistics and data analysis, converting decimals to fractions can be necessary for simplifying and interpreting data.
-
Everyday Life: From splitting bills to measuring ingredients, a grasp of decimal-to-fraction conversions is helpful in numerous daily situations.
Advanced Concepts: Recurring Decimals and Fractions
While 0.04 is a terminating decimal (it has a finite number of digits), not all decimals are. Recurring decimals, like 0.333... (one-third), require a different approach to conversion. These decimals have digits that repeat infinitely. To convert recurring decimals to fractions, a slightly more complex process is needed, often involving algebraic manipulation.
Troubleshooting Common Mistakes
When converting decimals to fractions, some common mistakes can be avoided with careful attention:
-
Incorrect Place Value: Ensure you correctly identify the place value of the last digit in the decimal (tenths, hundredths, thousandths, etc.). This determines the denominator of your initial fraction.
-
Failure to Simplify: Always simplify your fraction to its lowest terms. This is essential for clarity and ease of use in further calculations.
-
Improper Simplification: Ensure that you divide both the numerator and denominator by their greatest common divisor, not just any common divisor.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting decimals to fractions is a skill that builds a solid foundation for more advanced mathematical concepts. By understanding the place value system, employing simplification techniques, and appreciating the practical applications of this conversion, you'll greatly improve your mathematical proficiency. The conversion of 0.04 to 1/25 is a straightforward example, but mastering this process allows you to tackle more complex decimal-to-fraction problems with confidence. Remember to practice regularly and pay attention to detail to avoid common mistakes. With consistent effort, you'll soon be adept at converting decimals to fractions and confidently applying this skill in diverse contexts. This skill isn't just confined to the classroom; it's a vital tool for navigating various aspects of everyday life and professional fields.
Latest Posts
Latest Posts
-
Sr Oh 2 Strong Or Weak
Apr 01, 2025
-
A Bond In Which Electrons Are Shared Unequally
Apr 01, 2025
-
Greatest Common Factor Of 32 And 36
Apr 01, 2025
-
Least Common Multiple Of 4 And 30
Apr 01, 2025
-
The Principle Of Probability Can Be Used To
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction For 0.04 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
