What Is The Fourth Root Of 16
listenit
Mar 26, 2025 · 6 min read
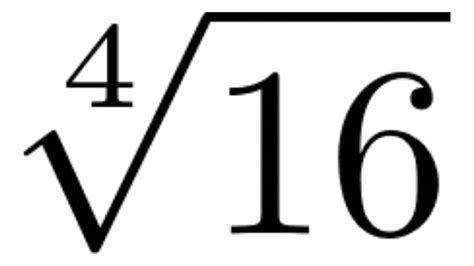
Table of Contents
What is the Fourth Root of 16? A Deep Dive into Roots, Radicals, and Beyond
The seemingly simple question, "What is the fourth root of 16?" opens a door to a fascinating world of mathematics, exploring concepts fundamental to algebra, calculus, and even more advanced fields. This article will delve into not just the answer but the underlying principles, exploring various methods of solving for roots, discussing the complexities of even versus odd roots, and touching upon the broader applications of these concepts.
Understanding Roots and Radicals
Before tackling the fourth root of 16, let's solidify our understanding of roots and radicals. A root is essentially the inverse operation of exponentiation. If we have a number, x, raised to the power of n (xⁿ), then the nth root of xⁿ is x. We express this using radical notation:
√ⁿxⁿ = x
Where:
- √ is the radical symbol.
- n is the index (the root we're taking – e.g., square root, cube root, fourth root).
- xⁿ is the radicand (the number under the radical).
For our specific problem, we're looking for the fourth root of 16, which is written as:
√⁴16
Solving for the Fourth Root of 16: Method 1 – Prime Factorization
One effective way to find the fourth root of 16 involves prime factorization. This method breaks down the number into its prime factors, making it easier to identify the root.
-
Prime Factorize 16: We find the prime factors of 16: 16 = 2 x 2 x 2 x 2 = 2⁴
-
Apply the Root: Since we're looking for the fourth root, we're essentially asking: what number, when multiplied by itself four times, equals 16? From the prime factorization, it's clear that this number is 2.
-
Solution: Therefore, √⁴16 = 2
Solving for the Fourth Root of 16: Method 2 – Exponents and Fractional Exponents
Another powerful method leverages the relationship between roots and exponents. The nth root of a number x can be expressed as x<sup>1/n</sup>. Therefore, the fourth root of 16 can be written as:
16<sup>1/4</sup>
This fractional exponent indicates that we need to find the fourth root. We can solve this using the following steps:
-
Rewrite 16 as a Power of 2: 16 = 2⁴
-
Substitute and Simplify: Substitute this into the expression: (2⁴)<sup>1/4</sup>. Using the rule of exponents that (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>, we simplify: (2⁴)<sup>1/4</sup> = 2<sup>(4*1/4)</sup> = 2¹ = 2
-
Solution: Therefore, 16<sup>1/4</sup> = 2
This method elegantly demonstrates the inverse relationship between exponents and roots.
The Concept of Multiple Roots: Real and Complex Numbers
While we've found one solution (2), it's crucial to understand that depending on the index (n) of the root and the nature of the radicand, there might be multiple roots. Let's explore this concept further.
Even Roots vs. Odd Roots
The even roots (square root, fourth root, etc.) of positive real numbers have two possible real solutions (one positive and one negative), whereas odd roots (cube root, fifth root, etc.) of real numbers have only one real solution.
Consider the fourth root again: (-2)⁴ = 16, so -2 is also a solution. This makes intuitive sense; -2 multiplied by itself four times yields a positive result.
Therefore, the complete set of real solutions to the fourth root of 16 is {2, -2}.
The situation becomes more complex when considering the roots of negative numbers, especially even roots, which introduce complex numbers. The fourth root of -16, for example, involves complex numbers and solutions expressed in terms of i (the imaginary unit, where i² = -1). These solutions lie in the complex plane, a two-dimensional plane that extends beyond the realm of real numbers.
Extending the Concept: Higher-Order Roots and Applications
The principles discussed above extend to higher-order roots—fifth root, sixth root, and beyond. The methods of prime factorization and fractional exponents remain applicable. The number of real solutions depends on whether the index is even or odd and the sign of the radicand.
The calculation of roots is fundamental to numerous applications across various fields, including:
- Engineering: Calculating dimensions, forces, and other physical quantities.
- Physics: Solving equations describing motion, energy, and waves.
- Finance: Computing interest rates, compound growth, and discounted cash flows.
- Computer Science: Implementing algorithms, data structures, and simulations.
Understanding the Importance of Precision in Calculations
In many practical applications, obtaining an accurate root is crucial. Slight inaccuracies in calculating the root can lead to significant errors in the final results, especially in complex calculations.
Practical Examples Illustrating the Fourth Root
Let's solidify our understanding with a few more examples.
Example 1: Finding the fourth root of 81
Using prime factorization: 81 = 3 x 3 x 3 x 3 = 3⁴. Therefore, the fourth root of 81 is 3. The complete set of real solutions is {3, -3}.
Example 2: Finding the fourth root of 625
Using prime factorization: 625 = 5 x 5 x 5 x 5 = 5⁴. Therefore, the fourth root of 625 is 5. The complete set of real solutions is {5, -5}.
Example 3: Illustrating the Complex Roots
Let's examine the fourth root of -16. This is where complex numbers come into play. While we can't find a real number that, when multiplied by itself four times, yields -16, we can use complex numbers to find the solutions. The solutions involve the imaginary unit 'i' and are beyond the scope of this introductory exploration. This illustrates the richness and complexity of the mathematical world beyond the realm of simple real numbers.
Conclusion: The Fourth Root of 16 and Beyond
The question, "What is the fourth root of 16?" has led us on an exciting journey into the world of roots, radicals, and exponents. We've explored multiple methods for solving this seemingly simple problem, uncovering the underlying mathematical principles and their broader applications. Understanding the nuances of even and odd roots, and the introduction of complex numbers when dealing with negative radicands, highlights the richness and depth of mathematical concepts that even seemingly simple calculations can reveal. This foundational knowledge is vital for success in more advanced mathematical studies and diverse applications across various fields. Remember that while finding the principal root is often sufficient, it's essential to be aware of the existence of multiple solutions, especially when working with even-indexed roots. Further exploration into complex numbers and their applications will unlock even deeper understanding of these fundamental mathematical principles.
Latest Posts
Latest Posts
-
Whats The Atomic Number For Potassium
Mar 29, 2025
-
Lewis Structure Of Carbon Monoxide With Formal Charges
Mar 29, 2025
-
Weather Occurs In Which Layer Of The Atmosphere
Mar 29, 2025
-
Common Factors Of 24 And 48
Mar 29, 2025
-
How Far In Light Years Is Pluto From Earth
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fourth Root Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
