Common Factors Of 24 And 48
listenit
Mar 29, 2025 · 6 min read
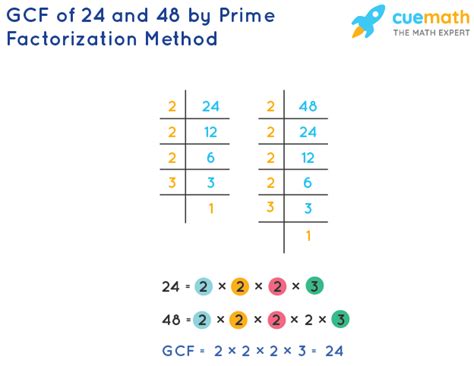
Table of Contents
Unlocking the Secrets of Factors: A Deep Dive into the Common Factors of 24 and 48
Finding the common factors of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in mathematics with broader implications in various fields, from cryptography to computer science. This article delves deep into the common factors of 24 and 48, exploring not just the answer but also the underlying principles and practical applications. We'll uncover the methods for finding these factors, discuss the concept of greatest common factors (GCF), and examine how this knowledge extends beyond basic arithmetic.
Understanding Factors and Divisibility
Before diving into the specifics of 24 and 48, let's establish a clear understanding of what factors are. A factor of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Divisibility rules offer shortcuts for determining factors. Knowing these rules can significantly speed up the process of identifying factors, especially for larger numbers. Some common divisibility rules include:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if its last two digits are divisible by 4.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 6: A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
These rules are helpful when systematically finding all the factors of a number.
Finding the Factors of 24 and 48
Let's apply our understanding to find the factors of 24 and 48:
Factors of 24:
To find the factors of 24, we systematically check which whole numbers divide 24 without leaving a remainder:
1, 2, 3, 4, 6, 8, 12, and 24.
Factors of 48:
Similarly, for 48, we find the following factors:
1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.
Identifying Common Factors
Now that we have the factors of both 24 and 48, we can identify the common factors, which are the numbers that appear in both lists:
1, 2, 3, 4, 6, 8, 12, and 24. These are all the numbers that divide both 24 and 48 without leaving a remainder.
Therefore, the common factors of 24 and 48 are 1, 2, 3, 4, 6, 8, 12, and 24.
The Greatest Common Factor (GCF)
Among the common factors, the greatest common factor (GCF), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. In this case, the GCF of 24 and 48 is 24. Finding the GCF is often crucial in various mathematical applications.
There are several methods for finding the GCF, including:
- Listing factors: As we did above, listing all factors and identifying the largest common one. This method is efficient for smaller numbers.
- Prime factorization: This involves breaking down each number into its prime factors (factors that are only divisible by 1 and themselves). The GCF is then found by multiplying the common prime factors raised to the lowest power. For 24 (2³ x 3) and 48 (2⁴ x 3), the common prime factors are 2³ and 3, resulting in a GCF of 2³ x 3 = 24.
- Euclidean algorithm: This is an efficient algorithm for finding the GCF of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Applications of Common Factors and GCF
Understanding common factors and the GCF extends beyond basic arithmetic and finds practical applications in various areas:
-
Simplifying fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 48/24 can be simplified to 2/1 (or simply 2) by dividing both the numerator and denominator by their GCF (24).
-
Solving problems involving groups: Consider a scenario where you have 24 apples and 48 oranges, and you want to divide them into equal-sized groups. The GCF (24) tells you the largest possible group size you can create using all the fruit. You can create 24 groups, each with one apple and two oranges.
-
Geometry: The GCF can be used in geometry problems involving area and perimeter calculations, simplifying expressions, and determining the dimensions of shapes.
-
Cryptography: The concept of GCF and prime factorization forms the basis of many cryptographic algorithms used to secure online communications and data.
-
Computer Science: The GCF and related algorithms are crucial in computer programming for tasks like simplifying expressions, optimizing code, and solving various algorithmic problems.
Beyond the Basics: Exploring Related Concepts
Understanding common factors leads to a deeper appreciation of other mathematical concepts:
-
Least Common Multiple (LCM): While we've focused on the GCF, the least common multiple (LCM) is another important concept. The LCM is the smallest number that is a multiple of both numbers. For 24 and 48, the LCM is 48. The GCF and LCM are related; their product equals the product of the two original numbers (GCF x LCM = 24 x 48 = 1152).
-
Modular Arithmetic: Modular arithmetic deals with remainders after division. Understanding factors plays a crucial role in modular arithmetic, used in various applications, including cryptography and computer science.
-
Number Theory: The study of factors, divisibility, and related concepts is a core part of number theory, a branch of mathematics with many advanced and unsolved problems.
Conclusion: The Significance of Simple Arithmetic
Finding the common factors of 24 and 48 might appear to be a simple exercise, but it underpins many advanced mathematical and computational concepts. Mastering this fundamental understanding not only helps you solve arithmetic problems but also lays the groundwork for a deeper appreciation of the interconnectedness of mathematical ideas and their practical relevance in various fields. The ability to quickly and efficiently find common factors and the GCF is a valuable skill that extends beyond the classroom into diverse applications in the world around us. Understanding these concepts empowers you to tackle more complex mathematical problems and appreciate the elegant beauty of fundamental arithmetic principles.
Latest Posts
Latest Posts
-
What Is To The 1 2 Power
Apr 01, 2025
-
Is Water Evaporating A Chemical Or Physical Change
Apr 01, 2025
-
Which Two Elements Make Up Water
Apr 01, 2025
-
How To Find A Unit Vector
Apr 01, 2025
-
What Is The Least Common Multiple Of 5 And 10
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 24 And 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
