What Is The Difference Between A Ratio And Rate
listenit
Mar 31, 2025 · 6 min read
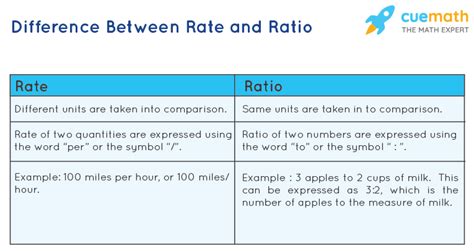
Table of Contents
What's the Difference Between a Ratio and a Rate? A Deep Dive
Understanding the nuances between ratios and rates is crucial for anyone working with numerical data, from students grappling with math concepts to professionals analyzing financial reports or scientific experiments. While seemingly similar at first glance, these two mathematical concepts possess distinct characteristics and applications. This comprehensive guide will delve into the core differences between ratios and rates, clarifying their definitions, providing illustrative examples, and highlighting their practical uses across various fields.
Defining Ratios: Comparing Quantities
A ratio is a mathematical comparison of two or more quantities of the same unit. It expresses the relative sizes of the quantities. Think of it as a way to quantify how much of one thing there is in relation to another. The key takeaway here is the sameness of units. You're not comparing apples and oranges; you're comparing apples to apples (or oranges to oranges).
Key Characteristics of Ratios:
- Comparison of like quantities: The fundamental aspect of a ratio is that it compares quantities measured in the same units. This could be anything from the number of boys to girls in a class, the proportion of red to blue marbles in a bag, or the ratio of ingredients in a recipe (e.g., flour to sugar).
- Expressing relative size: Ratios don't provide an absolute measurement; instead, they show the relationship between quantities. A ratio of 2:1 means there are twice as many of one quantity as the other.
- Multiple representations: Ratios can be expressed in several ways:
- Using a colon: 2:3 (read as "two to three")
- As a fraction: 2/3
- Using the word "to": 2 to 3
- Simplification: Like fractions, ratios can be simplified to their lowest terms. For instance, the ratio 6:9 can be simplified to 2:3 by dividing both numbers by their greatest common divisor (3).
Examples of Ratios:
- Recipe ratios: A cake recipe might call for a ratio of 2:1 flour to sugar.
- Student-teacher ratios: A school might have a student-teacher ratio of 20:1.
- Financial ratios: In finance, ratios like the debt-to-equity ratio are used to assess a company's financial health.
- Mixing ratios: A painter might mix paint in a ratio of 3:1 blue to white.
Defining Rates: Comparing Quantities with Different Units
A rate, on the other hand, is a special type of ratio that compares two quantities with different units. This crucial distinction separates it from a simple ratio. A rate expresses the relationship between quantities measured in different units, often involving a change over time.
Key Characteristics of Rates:
- Comparison of unlike quantities: Unlike ratios, rates compare quantities with different units. This could be speed (miles per hour), price (dollars per pound), or density (grams per cubic centimeter).
- Involving a change over time (often): Many rates involve a change over time, such as speed (distance per unit of time), growth rate (percentage change per unit of time), or consumption rate (units consumed per unit of time). However, not all rates are time-based.
- Units are crucial: The units of a rate are essential for understanding its meaning. The rate "60 miles per hour" is very different from "60 miles per minute."
- Can be simplified: Similar to ratios, rates can be simplified to make them easier to understand and use.
Examples of Rates:
- Speed: 60 miles per hour (miles/hour)
- Price: $2.50 per pound (dollars/pound)
- Heart rate: 72 beats per minute (beats/minute)
- Growth rate: 5% per year (percentage/year)
- Fuel efficiency: 30 miles per gallon (miles/gallon)
- Population density: 1000 people per square kilometer (people/km²)
The Crucial Difference: Units and Context
The core difference between a ratio and a rate boils down to the units of the quantities being compared. Ratios compare like quantities (same units), while rates compare unlike quantities (different units). The context in which the comparison is made also plays a significant role.
Consider these examples:
- Ratio: The ratio of boys to girls in a class is 15:12. Both quantities (boys and girls) are measured in the same unit – the number of students.
- Rate: The speed of a car is 60 miles per hour. Here, we're comparing distance (miles) and time (hours), which are different units.
Practical Applications: Ratios and Rates in Real Life
Ratios and rates are ubiquitous in everyday life and professional contexts. Let's explore some examples:
Ratios in Everyday Life:
- Cooking: Recipe ratios guide the proportions of ingredients to ensure consistent results.
- Scale models: Architects and model builders use ratios to create scaled-down representations of structures.
- Map scales: Maps employ ratios to represent distances on the ground in relation to distances on the map.
Rates in Various Fields:
- Finance: Interest rates, exchange rates, and various financial ratios are essential tools for investment analysis.
- Science: Reaction rates, growth rates, and density are all crucial concepts in scientific research and experimentation.
- Engineering: Engineers use rates to design systems that involve flow rates, speed, and power consumption.
- Healthcare: Heart rate, respiration rate, and various other vital signs are crucial for monitoring patient health.
Advanced Concepts and Considerations
While the basic difference between ratios and rates is straightforward, more complex scenarios might require a deeper understanding. Consider these points:
- Unit conversion: Often, rates involve unit conversion to express them in a more meaningful way. For example, converting miles per hour to kilometers per hour.
- Proportions: Both ratios and rates are fundamental to solving proportions – equations that state that two ratios or rates are equal.
- Dimensional analysis: Understanding dimensions (units) is critical for correctly working with both ratios and rates, especially in science and engineering. Dimensional analysis helps ensure that units cancel out correctly in calculations.
- Rates of change: In calculus, the concept of rates of change is essential. This involves determining how quickly a quantity is changing with respect to another quantity, often with respect to time.
Conclusion: Mastering the Distinction
The distinction between ratios and rates, while seemingly subtle, is crucial for clear communication and accurate calculations across numerous disciplines. By understanding the fundamental difference—the comparison of like quantities versus unlike quantities—and the implications of this difference regarding units, you can confidently apply these concepts in various real-world situations. This ability to discern and utilize ratios and rates effectively will enhance your problem-solving capabilities and deepen your understanding of numerical data. Remembering the units is key to correctly identifying whether you're dealing with a ratio or a rate. Mastering these concepts is a valuable skill for anyone seeking to improve their mathematical understanding and apply it practically.
Latest Posts
Latest Posts
-
Atoms Have No Electric Charge Because They
Apr 02, 2025
-
How Do You Find The Slope Of A Line Perpendicular
Apr 02, 2025
-
Divide 2x2 17x 35 By X 5
Apr 02, 2025
-
Number Of Valence Electrons For Carbon
Apr 02, 2025
-
How To Find Density Of A Solution
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Difference Between A Ratio And Rate . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
