Divide 2x2 + 17x + 35 By X + 5.
listenit
Apr 02, 2025 · 6 min read
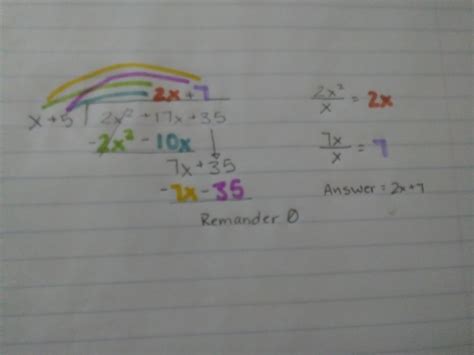
Table of Contents
Dividing 2x² + 17x + 35 by x + 5: A Comprehensive Guide
Polynomial division can seem daunting at first, but with a systematic approach, it becomes manageable and even enjoyable. This article will walk you through the process of dividing the polynomial 2x² + 17x + 35 by the binomial x + 5, explaining each step in detail and providing helpful tips and tricks along the way. We'll explore various methods, including long division and synthetic division, and discuss their applications in different scenarios. We'll also examine the broader context of polynomial division within algebra and its practical uses.
Understanding Polynomial Division
Before diving into the specific problem, let's establish a firm understanding of the concept of polynomial division. Essentially, it's the process of dividing one polynomial by another to find a quotient and a remainder. This is analogous to dividing whole numbers, where the dividend is divided by the divisor to get a quotient and a possible remainder. In the case of polynomials, the dividend is the polynomial being divided (in our case, 2x² + 17x + 35), and the divisor is the polynomial doing the dividing (x + 5). The result will consist of a quotient (another polynomial) and a remainder (which may be zero or another polynomial of lower degree than the divisor).
The fundamental theorem of algebra underpins this process, stating that every non-constant polynomial with complex coefficients has at least one complex root. This means that every polynomial can be factored into linear terms (of the form (x-a)), which facilitates polynomial division.
Method 1: Long Division
Long division is a classic and versatile method for dividing polynomials. While it might appear lengthy, it provides a clear visual representation of the division process and is especially helpful when dealing with higher-degree polynomials or divisors that aren't simple binomials.
Let's apply long division to divide 2x² + 17x + 35 by x + 5:
2x + 7
x + 5 | 2x² + 17x + 35
- (2x² + 10x)
7x + 35
- (7x + 35)
0
Step-by-step explanation:
-
Set up the long division: Arrange the dividend (2x² + 17x + 35) and divisor (x + 5) as shown above.
-
Divide the leading terms: Divide the leading term of the dividend (2x²) by the leading term of the divisor (x). This gives 2x, which is the first term of the quotient. Write this above the dividend.
-
Multiply and subtract: Multiply the divisor (x + 5) by the first term of the quotient (2x) to get 2x² + 10x. Subtract this result from the dividend.
-
Bring down the next term: Bring down the next term from the dividend (+35).
-
Repeat the process: Divide the leading term of the new dividend (7x) by the leading term of the divisor (x). This gives 7, which is the next term of the quotient. Multiply the divisor by 7 and subtract the result.
-
Remainder: In this case, the remainder is 0. This means that x + 5 is a factor of 2x² + 17x + 35.
Therefore, the quotient is 2x + 7, and the remainder is 0. We can express this as:
2x² + 17x + 35 = (x + 5)(2x + 7)
Method 2: Synthetic Division
Synthetic division is a shorthand method for dividing polynomials, particularly useful when the divisor is a linear binomial (of the form x - c). It's significantly faster than long division but requires a bit of practice to master.
To use synthetic division to divide 2x² + 17x + 35 by x + 5, we first note that the divisor is of the form x - c, where c = -5. The process proceeds as follows:
-5 | 2 17 35
| -10 -35
----------------
2 7 0
Step-by-step explanation:
-
Write the coefficients: Write the coefficients of the dividend (2, 17, 35) in a row.
-
Bring down the first coefficient: Bring down the first coefficient (2).
-
Multiply and add: Multiply the first coefficient (2) by the divisor's constant (-5) to get -10. Add this to the second coefficient (17) to get 7.
-
Repeat: Multiply the result (7) by the divisor's constant (-5) to get -35. Add this to the last coefficient (35) to get 0.
The resulting numbers (2 and 7) are the coefficients of the quotient, and the last number (0) is the remainder. Thus, the quotient is 2x + 7, and the remainder is 0. This confirms the result obtained through long division.
Verifying the Result
It's always a good practice to verify the result of polynomial division. We can do this by multiplying the quotient by the divisor and adding the remainder. If the result equals the dividend, our division was correct.
(2x + 7)(x + 5) + 0 = 2x² + 10x + 7x + 35 = 2x² + 17x + 35
This matches our original dividend, confirming the accuracy of our calculations.
Applications of Polynomial Division
Polynomial division finds application in various areas of mathematics and beyond. Some key applications include:
-
Finding roots of polynomials: If the remainder is 0 after dividing a polynomial by a binomial (x - c), then 'c' is a root of the polynomial.
-
Factoring polynomials: Polynomial division helps in factoring complex polynomials into simpler forms, making it easier to analyze their properties.
-
Partial fraction decomposition: This technique, essential in calculus, uses polynomial division to simplify rational functions.
-
Solving equations: Polynomial division can simplify complex equations, making them easier to solve.
-
Engineering and science: Polynomial division is used in various engineering applications, such as signal processing, control systems, and modeling physical phenomena.
Advanced Concepts and Further Exploration
While we've focused on dividing a quadratic polynomial by a linear binomial, the principles of polynomial division extend to higher-degree polynomials and more complex divisors. Further exploration might involve:
-
Dividing polynomials with complex coefficients: The methods remain the same, but the calculations involve complex numbers.
-
Dividing polynomials with missing terms: It's crucial to account for missing terms by using zero as a placeholder coefficient.
-
Remainder Theorem and Factor Theorem: These theorems establish a powerful connection between polynomial division and the roots of a polynomial.
Conclusion
Mastering polynomial division, whether using long division or synthetic division, is a crucial skill in algebra and beyond. Understanding the underlying concepts and practicing different methods builds a strong foundation for tackling more advanced mathematical problems. Remember to always verify your results to ensure accuracy, and don't hesitate to explore the numerous applications of this fundamental algebraic technique. The systematic approach outlined in this article, along with consistent practice, will empower you to confidently tackle polynomial division problems of increasing complexity. By understanding the ‘why’ behind each step, you'll not only improve your problem-solving abilities but also gain a deeper appreciation for the elegance and power of algebra.
Latest Posts
Latest Posts
-
What Is A Reactant In Photosynthesis
Apr 03, 2025
-
32 Of 40 Percent Is What Number
Apr 03, 2025
-
What Is Found In Plant Cells But Not Animal Cells
Apr 03, 2025
-
What Percent Of 9 2 Is 43 7
Apr 03, 2025
-
What Is The Square Root Of 240
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Divide 2x2 + 17x + 35 By X + 5. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
