What Is The Derivative Of Ln5x
listenit
Mar 27, 2025 · 5 min read
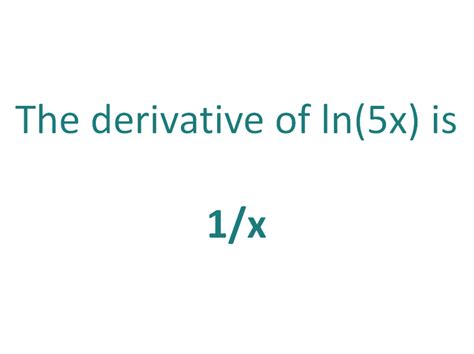
Table of Contents
What is the Derivative of ln(5x)? A Comprehensive Guide
The derivative of ln(5x) is a fundamental concept in calculus, frequently encountered in various applications. This comprehensive guide will not only provide the answer but will also delve into the underlying principles, demonstrate the steps involved in finding the derivative, and explore related concepts to solidify your understanding.
Understanding the Natural Logarithm and Differentiation
Before diving into the specifics of finding the derivative of ln(5x), let's briefly revisit the definitions of the natural logarithm and the process of differentiation.
The Natural Logarithm (ln(x))
The natural logarithm, denoted as ln(x), is the logarithm to the base e, where e is Euler's number, an irrational mathematical constant approximately equal to 2.71828. In simpler terms, ln(x) answers the question: "To what power must e be raised to obtain x?" For example, ln(e) = 1 because e¹ = e. The natural logarithm is crucial in various fields, including calculus, physics, and finance, due to its unique properties and its relationship with exponential functions.
Differentiation: Finding the Rate of Change
Differentiation is a fundamental operation in calculus that determines the instantaneous rate of change of a function. Geometrically, the derivative at a point represents the slope of the tangent line to the function's graph at that point. The derivative of a function f(x) is typically denoted as f'(x), df/dx, or dy/dx.
Finding the Derivative of ln(5x)
Now, let's tackle the core problem: finding the derivative of ln(5x). We will utilize the chain rule, a crucial rule in differentiation.
The Chain Rule
The chain rule states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) times the derivative of the inside function. Mathematically:
d/dx [f(g(x))] = f'(g(x)) * g'(x)
In our case, the composite function is ln(5x), where the outer function is ln(u) and the inner function is u = 5x.
Applying the Chain Rule to ln(5x)
-
Identify the outer and inner functions:
- Outer function: f(u) = ln(u)
- Inner function: g(x) = 5x
-
Find the derivatives of the outer and inner functions:
- Derivative of the outer function: f'(u) = 1/u (The derivative of ln(u) is 1/u)
- Derivative of the inner function: g'(x) = 5 (The derivative of 5x is 5)
-
Apply the chain rule:
- Substitute u = 5x into f'(u): f'(g(x)) = 1/(5x)
- Multiply the derivatives: (1/(5x)) * 5 = 1/x
Therefore, the derivative of ln(5x) is 1/x.
Step-by-Step Breakdown with Explanations
Let's break down the process even further, addressing potential points of confusion.
-
Begin with the function: We start with the function y = ln(5x).
-
Apply the chain rule: Remember the chain rule: d/dx[f(g(x))] = f'(g(x)) * g'(x). Here, f(u) = ln(u) and g(x) = 5x.
-
Differentiate the outer function: The derivative of ln(u) with respect to u is 1/u. So, f'(u) = 1/u.
-
Differentiate the inner function: The derivative of 5x with respect to x is 5. So, g'(x) = 5.
-
Substitute and multiply: We substitute g(x) (which is 5x) into f'(u): f'(g(x)) = 1/(5x). Then, we multiply this by the derivative of the inner function: (1/(5x)) * 5 = 1/x.
-
Final Result: The derivative of ln(5x) is therefore dy/dx = 1/x.
Illustrative Examples and Applications
Understanding the derivative of ln(5x) is crucial for solving various calculus problems. Let's illustrate this with a couple of examples.
Example 1: Finding the Slope of a Tangent Line
Let's say we want to find the slope of the tangent line to the curve y = ln(5x) at x = 2.
-
Find the derivative: We already know that dy/dx = 1/x.
-
Evaluate at x = 2: Substitute x = 2 into the derivative: dy/dx = 1/2 = 0.5.
Therefore, the slope of the tangent line to the curve y = ln(5x) at x = 2 is 0.5.
Example 2: Optimization Problems
The derivative is essential in optimization problems. Imagine a scenario where the cost function of producing x units is given by C(x) = 100 + 50ln(5x). To find the marginal cost (the cost of producing one additional unit), we need to find the derivative of C(x):
- Find the derivative: dC/dx = d/dx [100 + 50ln(5x)] = 0 + 50 * (1/x) = 50/x
Thus, the marginal cost is 50/x. This allows businesses to analyze how the cost changes as production increases.
Understanding the Implications and Further Exploration
The simplicity of the derivative of ln(5x) belies its importance. This derivative, 1/x, forms the basis for solving many more complex problems in calculus and its applications. Understanding the chain rule and its application in this context is fundamental for mastering more advanced calculus concepts.
Furthermore, exploring the integral counterpart of this derivative (the indefinite integral of 1/x, which is ln|x| + C) deepens your understanding of the relationship between differentiation and integration. This interplay is a cornerstone of calculus, highlighting the interconnectedness of these fundamental operations.
Conclusion
Finding the derivative of ln(5x) involves a straightforward application of the chain rule, resulting in the simple yet powerful expression 1/x. Understanding this derivation is not only crucial for solving specific calculus problems but also serves as a stepping stone to mastering more complex techniques and applying calculus to various real-world scenarios. The examples provided illustrate its practical applications in diverse fields, highlighting its significance beyond theoretical exercises. Continuously practicing and applying these concepts is key to strengthening your understanding and mastering the fundamentals of calculus.
Latest Posts
Latest Posts
-
0 6 As A Fraction In Simplest Form
Mar 30, 2025
-
What Is The Only Liquid Layer Of The Earth
Mar 30, 2025
-
What The Molecular Shape Geometry Of Chclo
Mar 30, 2025
-
What Is The Atomic Number Of An Atom Equivalent To
Mar 30, 2025
-
Diameter Of Solar System In Light Years
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Derivative Of Ln5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
