What Is The Circumference Of A Circle With Radius 3
listenit
Apr 02, 2025 · 5 min read
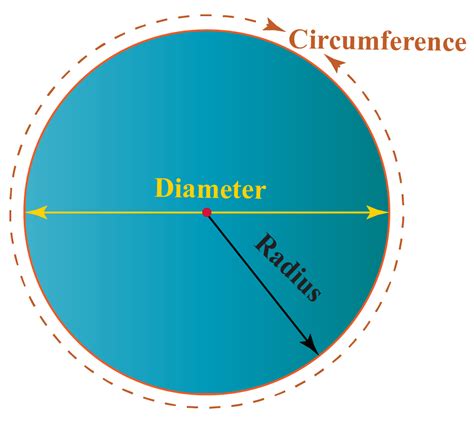
Table of Contents
What is the Circumference of a Circle with Radius 3? A Deep Dive into Circular Geometry
The question, "What is the circumference of a circle with radius 3?" might seem simple at first glance. It's a fundamental problem in geometry, easily solvable with a straightforward formula. However, exploring this seemingly simple question opens a door to a deeper understanding of circles, their properties, and the fascinating world of mathematical constants like π (pi). This article will not only provide the answer but also delve into the concepts, derivations, and applications surrounding circular geometry, ensuring a comprehensive understanding for both beginners and those seeking a refresher.
Understanding the Fundamentals: Radius, Diameter, and Circumference
Before we calculate the circumference, let's establish the key terms involved. A circle is a perfectly round two-dimensional shape where every point on its boundary is equidistant from a central point called the center. The radius is the distance from the center to any point on the circle. The diameter is the distance across the circle, passing through the center; it's simply twice the radius. Finally, the circumference is the distance around the circle.
In our case, we're given a radius of 3 units (it could be 3 centimeters, 3 meters, 3 inches – the unit doesn't affect the calculation). Therefore, the diameter is 2 * 3 = 6 units.
The Formula: Connecting Radius and Circumference
The relationship between the radius (or diameter) and the circumference of a circle is defined by a crucial mathematical constant: π (pi). Pi is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. It's an irrational number, meaning its decimal representation goes on forever without repeating.
The formula for the circumference (C) of a circle with radius (r) is:
C = 2πr
Alternatively, using the diameter (d), the formula is:
C = πd
Both formulas are equivalent, as d = 2r.
Calculating the Circumference: A Step-by-Step Approach
Now, let's calculate the circumference of our circle with a radius of 3:
-
Identify the radius: r = 3 units
-
Use the formula: C = 2πr
-
Substitute the value: C = 2 * π * 3
-
Simplify: C = 6π units
This is the exact circumference. If we need a numerical approximation, we can use the approximate value of π ≈ 3.14159:
C ≈ 6 * 3.14159 ≈ 18.84954 units
Therefore, the circumference of a circle with a radius of 3 units is approximately 18.85 units.
Beyond the Basics: Exploring the Significance of Pi
The constant π is far more than just a number used in the circumference formula. It appears in countless mathematical formulas and has profound implications across various fields:
-
Trigonometry: Pi is fundamental in trigonometric functions like sine, cosine, and tangent, which describe relationships between angles and sides of triangles.
-
Calculus: Pi is integral to numerous calculus concepts, including integration and differentiation, used to solve complex problems in physics, engineering, and economics.
-
Probability and Statistics: Pi surprisingly appears in probability distributions, shaping our understanding of randomness and statistical analysis.
-
Physics: Pi plays a crucial role in describing phenomena involving circular or wave-like motion, such as planetary orbits, wave propagation, and oscillations.
-
Engineering: From designing wheels and gears to calculating the volume of cylindrical tanks, pi is essential in various engineering disciplines.
Applications of Circumference Calculations: Real-World Examples
The ability to calculate the circumference has countless practical applications in various fields:
-
Construction and Engineering: Determining the amount of materials needed for circular structures like roads, tracks, or pipelines.
-
Manufacturing: Calculating the length of materials required for circular components in machinery and products.
-
Agriculture: Estimating the amount of fencing needed for circular fields or irrigation systems.
-
Cartography: Calculating distances on maps that involve circular paths or curved geographical features.
-
Astronomy: Determining the distances involved in planetary orbits or the sizes of celestial bodies.
Advanced Concepts: Area of a Circle and Related Formulas
While we focused on circumference, let's briefly touch upon another crucial aspect of circles – their area. The formula for the area (A) of a circle with radius (r) is:
A = πr²
For our circle with radius 3, the area would be:
A = π * 3² = 9π ≈ 28.27 square units.
Understanding the area and circumference allows for calculations of other related parameters like the arc length of a sector, the area of a segment, and the properties of inscribed and circumscribed figures.
Approximating Pi: A Historical Perspective
The precise value of π has been a subject of fascination and pursuit for centuries. Ancient civilizations employed different methods to approximate its value, leading to progressively more accurate estimations. From the Egyptians' approximation of 3.16 to Archimedes' method using polygons, the quest to determine π has significantly contributed to the development of mathematics. Today, computers have calculated π to trillions of digits, yet its full value remains elusive, reflecting the enduring mystery and importance of this mathematical constant.
Conclusion: More Than Just a Simple Calculation
The simple question of calculating the circumference of a circle with a radius of 3 has led us on a journey through the fascinating world of circular geometry, the importance of π, and its widespread applications. The answer, approximately 18.85 units, is just the tip of the iceberg. A deeper understanding of these concepts empowers us to solve complex problems and appreciate the elegance and power of mathematics in our daily lives. The ability to calculate circumference is not merely an academic exercise; it is a practical skill with tangible real-world applications across diverse fields. This exploration should encourage a continued pursuit of mathematical knowledge and an appreciation for the underlying principles that shape our world.
Latest Posts
Latest Posts
-
X 3y 9 In Slope Intercept Form
Apr 03, 2025
-
What State Of Matter Is Electricity
Apr 03, 2025
-
What Percent Is 26 Out Of 30
Apr 03, 2025
-
What Percent Of 84 Is 21
Apr 03, 2025
-
The Change In State From Liquid To Gas Is Called
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Circumference Of A Circle With Radius 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
