What Is Square Root Of 65
listenit
Mar 31, 2025 · 4 min read
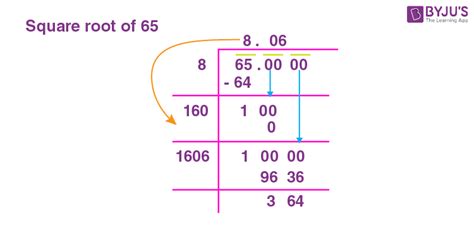
Table of Contents
What is the Square Root of 65? A Deep Dive into Irrational Numbers and Approximations
The question, "What is the square root of 65?" seems simple enough. However, delving into this seemingly straightforward mathematical problem reveals a fascinating exploration of irrational numbers, approximation methods, and the beauty of mathematics itself. This article will not only answer the question directly but also explore the underlying concepts and practical applications.
Understanding Square Roots
Before diving into the square root of 65, let's establish a foundational understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9. This concept is fundamental to many areas of mathematics, science, and engineering.
Why the Square Root of 65 is Irrational
Unlike the square root of 9, which is a whole number (3), the square root of 65 (√65) is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation goes on forever without repeating. This is a key characteristic of many square roots, particularly those of non-perfect squares (numbers that aren't the product of an integer multiplied by itself).
The proof that √65 is irrational involves a technique called proof by contradiction. We assume √65 is rational, meaning it can be expressed as a fraction a/b where a and b are integers and b is not zero. Through algebraic manipulation, we can demonstrate this leads to a contradiction, proving our initial assumption was false. Therefore, √65 must be irrational. This subtle yet powerful demonstration highlights the elegance and rigor of mathematical proofs.
Calculating the Square Root of 65: Methods and Approximations
Since we can't express √65 as a simple fraction or a terminating decimal, we must rely on approximation methods. Several techniques exist, ranging from simple estimation to sophisticated algorithms used in computers.
1. Estimation
A simple estimation can be achieved by recognizing that 65 lies between the perfect squares 64 (8²) and 81 (9²). Therefore, √65 must be between 8 and 9. A more refined estimate can be made by considering the proximity of 65 to 64. Since 65 is closer to 64 than to 81, we can guess that √65 is slightly larger than 8.
2. Babylonian Method (Heron's Method)
This iterative method provides increasingly accurate approximations. The formula is:
x_(n+1) = 0.5 * (x_n + S/x_n)
Where:
- x_n is the current approximation
- x_(n+1) is the next approximation
- S is the number whose square root we want to find (in this case, 65)
Let's use this method:
-
Start with an initial guess: Let's start with x_1 = 8 (our initial estimation).
-
Iterate:
- x_2 = 0.5 * (8 + 65/8) ≈ 8.0625
- x_3 = 0.5 * (8.0625 + 65/8.0625) ≈ 8.0622577
- x_4 = 0.5 * (8.0622577 + 65/8.0622577) ≈ 8.0622577 (convergence is reached)
As you can see, the method quickly converges to a highly accurate approximation.
3. Using a Calculator or Computer
Modern calculators and computers employ sophisticated algorithms, often variations of the Newton-Raphson method (a generalization of the Babylonian method), to calculate square roots to a high degree of accuracy. These methods are significantly faster and more efficient than manual calculations. Using a calculator, we find that:
√65 ≈ 8.062257748
Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous practical applications across various fields:
- Physics: Calculating velocity, acceleration, and energy often involves square roots.
- Engineering: Determining the dimensions of structures, analyzing stress and strain, and calculating electrical impedance frequently use square roots.
- Geometry: Finding the lengths of diagonals, calculating areas and volumes of shapes (like the diagonal of a square or the hypotenuse of a right triangle using the Pythagorean theorem), and working with circles and spheres involves square root calculations.
- Finance: Calculating investment returns and determining standard deviation in financial modeling.
- Computer Graphics: Used extensively in transformations, rotations, and calculations involving 2D and 3D coordinates.
- Statistics: Calculating standard deviation and variance, essential concepts in data analysis.
Exploring Related Concepts
Understanding the square root of 65 opens doors to exploring related mathematical concepts:
- Perfect Squares: Numbers that are the square of an integer (e.g., 1, 4, 9, 16...). Understanding these helps in estimations.
- Irrational Numbers: Numbers that cannot be expressed as a fraction of two integers. √65 is a prime example. Other famous irrational numbers include π (pi) and e (Euler's number).
- Approximation Methods: Various techniques, like the Babylonian method and Newton-Raphson method, demonstrate the power of iterative algorithms to solve complex problems.
- Numerical Analysis: The study of algorithms for obtaining numerical solutions to mathematical problems, including square root calculations.
Conclusion
The seemingly simple question, "What is the square root of 65?" leads to a rich exploration of mathematical concepts. While we cannot express √65 as an exact fraction or terminating decimal, we can approximate its value using various methods, from simple estimation to sophisticated algorithms. The irrationality of √65 underscores the beauty and complexity of the number system. Understanding square roots and related concepts is crucial for success in various fields, highlighting the importance of mathematical literacy. This article has hopefully provided a comprehensive overview, allowing you to not only understand the answer but also appreciate the underlying mathematical principles.
Latest Posts
Latest Posts
-
Which Organelles Supply Energy To The Cell
Apr 02, 2025
-
Why Is Density A Physical Property
Apr 02, 2025
-
Is Koh A Base Or Acid
Apr 02, 2025
-
Why Did Small States Object To The Virginia Plan
Apr 02, 2025
-
What Is The Proper Name For Mgf2
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
