What Is Lcm Of 5 And 6
listenit
Apr 01, 2025 · 4 min read
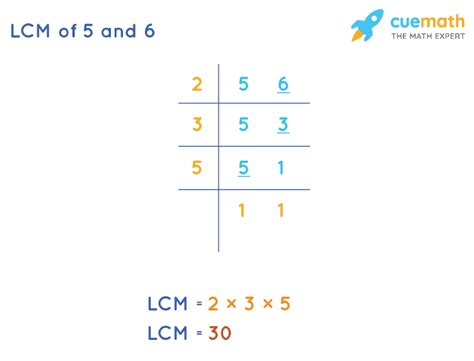
Table of Contents
What is the LCM of 5 and 6? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even music theory. This article will comprehensively explore how to calculate the LCM of 5 and 6, and then delve deeper into the broader context of LCMs, providing various methods for calculation and highlighting their applications.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 5 and 6, let's establish a firm understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
Key characteristics of the LCM:
- Positive Integer: The LCM is always a positive whole number.
- Divisibility: The LCM is divisible by each of the given numbers.
- Smallest: It's the smallest positive integer satisfying the divisibility condition.
Calculating the LCM of 5 and 6: Three Proven Methods
Now, let's find the LCM of 5 and 6 using three different approaches:
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest multiple common to both.
Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
Multiples of 6: 6, 12, 18, 24, 30, 36...
Notice that 30 is the smallest number that appears in both lists. Therefore, the LCM of 5 and 6 is 30.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiply these together: 2 x 3 x 5 = 30. Thus, the LCM of 5 and 6 is 30.
Method 3: Using the Formula (For Two Numbers)
For two numbers, a and b, there's a handy formula that relates the LCM and the Greatest Common Divisor (GCD):
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 5 and 6. Since 5 is a prime number and 6 is not divisible by 5, the GCD of 5 and 6 is 1.
Now, we apply the formula:
LCM(5, 6) = (5 x 6) / 1 = 30
This confirms our previous results.
Beyond the Basics: LCM for More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The listing multiples method becomes less practical, but prime factorization remains highly effective. For example, let's find the LCM of 5, 6, and 10:
-
Prime factorization:
- 5 = 5
- 6 = 2 x 3
- 10 = 2 x 5
-
Identify highest powers:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
-
Multiply: 2 x 3 x 5 = 30
Therefore, the LCM of 5, 6, and 10 is 30.
Real-World Applications of LCM
The concept of LCM extends far beyond the realm of abstract mathematics. It finds practical applications in diverse fields:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions directly involves calculating the LCM of the denominators. For instance, adding 1/5 and 1/6 requires finding the LCM of 5 and 6 (which is 30), converting the fractions to have a common denominator, and then performing the addition.
2. Scheduling and Synchronization:
LCM is crucial in scheduling problems. Imagine two buses leaving a station at different intervals. The LCM of their intervals determines when they will depart simultaneously again. This principle is used extensively in various scheduling scenarios, from manufacturing processes to public transport.
3. Music Theory:
In music, the LCM is used to find the least common multiple of the rhythmic values (e.g., beats) to determine when different rhythmic patterns will align perfectly.
4. Engineering and Construction:
In scenarios involving repetitive processes or patterns, such as the arrangement of tiles or the design of repeating structures, the LCM helps determine the optimal repeating interval.
5. Computer Science:
LCM is used in algorithms related to process scheduling and resource allocation.
Conclusion: Mastering the LCM
Understanding the least common multiple is a vital mathematical skill with far-reaching applications. While simple for smaller numbers, mastering the prime factorization method allows for efficient calculation even with larger or multiple numbers. This article has provided a comprehensive overview, from basic calculation techniques to advanced applications, empowering you to confidently tackle LCM problems in various contexts. Remember, the key is to understand the underlying principles and select the most efficient method based on the specific problem at hand. Whether you're dealing with fractions, scheduling, or musical rhythms, the LCM plays a significant role in solving real-world problems.
Latest Posts
Latest Posts
-
How Many Grams In 8 Kilograms
Apr 02, 2025
-
12x 4y 20 Solve For Y
Apr 02, 2025
-
Most Reactive Group On The Periodic Table
Apr 02, 2025
-
How To Solve Multi Step Inequalities
Apr 02, 2025
-
Percent Composition Of Mg No3 2
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
