What Is 8/25 As A Decimal
listenit
Mar 31, 2025 · 5 min read
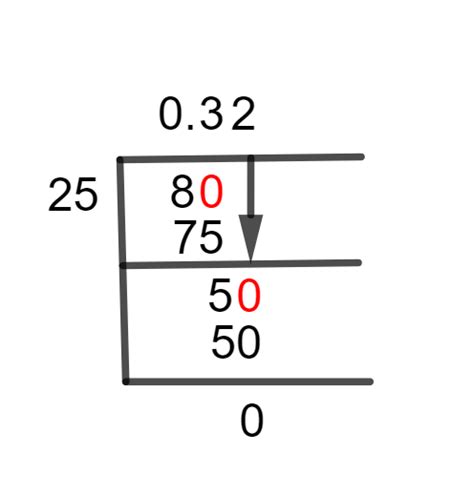
Table of Contents
What is 8/25 as a Decimal? A Comprehensive Guide to Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill in mathematics with broad applications across various fields. Understanding this process is crucial for anyone working with numerical data, from students tackling math problems to professionals using spreadsheets and data analysis tools. This comprehensive guide will delve deep into converting the fraction 8/25 into a decimal, explaining the process step-by-step and exploring various methods to achieve the same result. We'll also examine the broader context of fraction-to-decimal conversion and its significance.
Understanding Fractions and Decimals
Before we dive into the specific conversion of 8/25, let's quickly recap the concepts of fractions and decimals.
Fractions: A fraction represents a part of a whole. It consists of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For example, in the fraction 8/25, 8 is the numerator and 25 is the denominator.
Decimals: A decimal is a way of expressing a number using a base-10 system. The decimal point separates the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, 0.3 represents three-tenths, and 0.35 represents thirty-five hundredths.
Method 1: Direct Division
The most straightforward way to convert a fraction to a decimal is through direct division. We divide the numerator (8) by the denominator (25).
Step 1: Set up the long division problem: 8 ÷ 25
Step 2: Since 8 is smaller than 25, we add a decimal point to 8 and add a zero to make it 8.0.
Step 3: Now, we can perform the division: 25 goes into 80 three times (25 x 3 = 75).
Step 4: Subtract 75 from 80, leaving a remainder of 5.
Step 5: Add another zero to the remainder (50). 25 goes into 50 two times (25 x 2 = 50).
Step 6: Subtract 50 from 50, leaving a remainder of 0. The division is complete.
Therefore, 8/25 = 0.32
Method 2: Equivalent Fractions and Decimal Equivalents
This method involves converting the fraction to an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This makes the conversion to a decimal straightforward.
Step 1: Find a number that you can multiply the denominator (25) by to get a power of 10. In this case, we can multiply 25 by 4 to get 100 (25 x 4 = 100).
Step 2: Since we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the fraction's value. 8 x 4 = 32.
Step 3: This gives us the equivalent fraction 32/100.
Step 4: A fraction with a denominator of 100 can be easily converted to a decimal. The numerator (32) becomes the decimal part, with two decimal places (because the denominator is 100).
Therefore, 32/100 = 0.32
Method 3: Using a Calculator
The simplest method, especially for more complex fractions, is to use a calculator. Simply input the fraction as 8 ÷ 25, and the calculator will directly provide the decimal equivalent: 0.32
Understanding the Result: 0.32
The decimal 0.32 represents thirty-two hundredths. This is equivalent to 32/100, which, as we've seen, simplifies to 8/25. Understanding this equivalence is crucial in various mathematical applications.
Applications of Fraction-to-Decimal Conversion
The ability to convert fractions to decimals is fundamental in many areas:
-
Everyday Calculations: From calculating tips to splitting bills, understanding decimal representation of fractions is essential for daily life.
-
Finance: In finance, percentages (which are essentially fractions) are often represented as decimals. Calculating interest, returns on investments, and other financial metrics relies heavily on this conversion.
-
Science and Engineering: Many scientific measurements and calculations use decimal notation. Converting fractions to decimals allows for easier calculations and comparisons.
-
Computer Programming: Computers work with numerical data in binary format, but programming languages often require decimal input and output. Understanding fraction-to-decimal conversion is crucial in numerical computations within programs.
-
Data Analysis: Data analysis frequently involves working with numerical data, including fractions and percentages. Converting fractions to decimals enables easier analysis and manipulation of data using statistical software and spreadsheets.
Beyond 8/25: Converting Other Fractions
The methods discussed above can be applied to convert any fraction to a decimal. The key is to understand the underlying principles of division and the relationship between fractions and decimals. Here are some examples:
- 1/4: This is easily converted to 0.25 (divide 1 by 4).
- 3/8: This can be converted to 0.375 (divide 3 by 8).
- 2/3: This results in a repeating decimal: 0.6666... This highlights that not all fractions convert to terminating decimals.
Repeating Decimals and Terminating Decimals
It's important to note that not all fractions produce terminating decimals (decimals that end). Some fractions result in repeating decimals, which have a pattern of digits that repeat infinitely. For example, 1/3 = 0.3333... Understanding the difference between terminating and repeating decimals is crucial for advanced mathematical concepts.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a vital skill with wide-ranging applications. Whether you use direct division, equivalent fractions, or a calculator, understanding the underlying principles is key. This guide provided a detailed explanation of the conversion of 8/25 to 0.32, along with various methods and broader applications. Mastering this skill will enhance your mathematical proficiency and make it easier to navigate numerical tasks in various aspects of life and work. Practice makes perfect, so try converting different fractions to decimals using the methods discussed here to solidify your understanding. Remember, the more you practice, the more confident and efficient you'll become in tackling these types of problems.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 24 And 42
Apr 02, 2025
-
What 3 Particles Make Up An Atom
Apr 02, 2025
-
Blood Is What Type Of Mixture
Apr 02, 2025
-
What Is The Empirical Formula Of Ibuprofen
Apr 02, 2025
-
What Is One Sixth As A Decimal
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/25 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
