What Is 7/9 As A Percent
listenit
Apr 05, 2025 · 5 min read
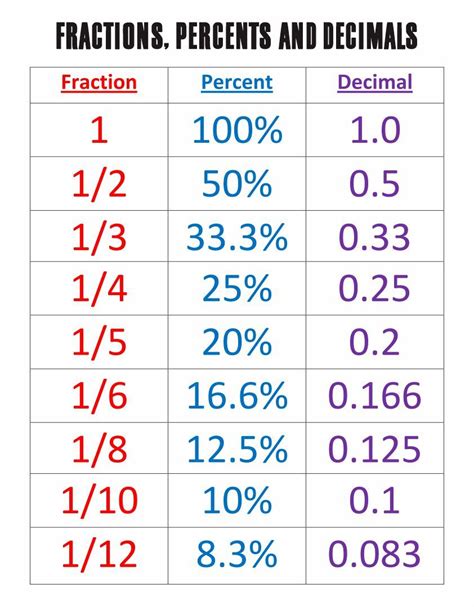
Table of Contents
What is 7/9 as a Percent? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 7/9 into a percentage, exploring different methods and providing a detailed explanation for a thorough understanding. We'll also look at how to use this knowledge in real-world scenarios and explore related mathematical concepts.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In the fraction 7/9, 7 is the numerator and 9 is the denominator. This means we have 7 parts out of a total of 9 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 7/9 to a percentage involves dividing the numerator by the denominator and then multiplying by 100.
-
Divide the numerator by the denominator: 7 ÷ 9 ≈ 0.777... (Note: this is a recurring decimal)
-
Multiply the result by 100: 0.777... × 100 ≈ 77.77...%
Therefore, 7/9 is approximately 77.78%. We round to two decimal places for practicality.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach is to find an equivalent fraction of 7/9 where the denominator is 100. This method, while less direct, reinforces the concept of equivalent fractions and provides a deeper understanding.
Unfortunately, there isn't a whole number that we can multiply 9 by to get 100. However, we can approximate. To do this, we can set up a proportion:
7/9 = x/100
To solve for x, we cross-multiply:
9x = 700
x = 700/9 ≈ 77.78
Therefore, 7/9 is approximately equal to 77.78/100, which is 77.78%.
Understanding Recurring Decimals
The conversion of 7/9 results in a recurring decimal (0.777...). A recurring decimal is a decimal number that has a digit or a sequence of digits that repeat infinitely. In this case, the digit "7" repeats infinitely. When dealing with recurring decimals in percentage calculations, rounding is necessary for practical application. The standard practice is to round to a reasonable number of decimal places, usually two, for percentage calculations.
Real-World Applications
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves working with fractions and percentages. For example, understanding that a 7/9 discount is approximately a 77.78% discount can greatly aid in financial decision-making.
-
Statistics: Percentages are frequently used to represent data and proportions in statistical analysis. Converting fractions to percentages makes it easier to interpret and compare data.
-
Everyday Life: Many everyday situations require converting fractions to percentages. For example, calculating the percentage of a task completed, expressing the proportion of ingredients in a recipe, or determining the success rate of an activity all involve these conversions.
-
Science: In scientific experiments and data analysis, expressing results as percentages often makes it easier to interpret and compare results from different experiments or groups.
Advanced Concepts and Related Topics
Understanding the conversion of 7/9 to a percentage opens doors to more advanced mathematical concepts:
-
Ratio and Proportion: The methods used to convert 7/9 to a percentage rely heavily on the concepts of ratio and proportion. Understanding these concepts is fundamental to various mathematical applications.
-
Decimal Representation of Fractions: Converting fractions to decimals, and vice-versa, is an essential skill in mathematics, directly related to percentage calculations.
-
Approximation and Rounding: Dealing with recurring decimals highlights the importance of approximation and rounding techniques for practical applications in real-world scenarios.
Troubleshooting Common Errors
While the conversion of 7/9 to a percentage is relatively straightforward, here are some common errors to avoid:
-
Incorrect Division: Ensure you divide the numerator (7) by the denominator (9) correctly. Using a calculator can help avoid this error.
-
Forgetting to Multiply by 100: Remember that the result of the division must be multiplied by 100 to obtain the percentage.
-
Incorrect Rounding: When dealing with recurring decimals, round the result to the appropriate number of decimal places, usually two for percentage calculations. Consistency in rounding is crucial for accuracy.
-
Misunderstanding the Concept of Percentage: Ensure you understand that a percentage represents a proportion out of 100.
Conclusion: Mastering Fraction-to-Percentage Conversion
Converting 7/9 to a percentage, which is approximately 77.78%, is a practical demonstration of a fundamental mathematical skill. Mastering this conversion, along with understanding related concepts like recurring decimals and approximation techniques, enhances mathematical proficiency and allows for efficient problem-solving in various real-world situations. By practicing different methods and understanding the underlying principles, you can confidently tackle similar conversions and apply this knowledge across a range of disciplines. The key is to practice regularly and to understand why each step is necessary in the conversion process. The more you practice, the more comfortable and efficient you will become. Remember, even seemingly simple mathematical problems can hold a wealth of underlying concepts that, once mastered, can significantly enhance your problem-solving capabilities and understanding of the world around us.
Latest Posts
Latest Posts
-
1 4 3 8 Reduced To The Lowest Terms
Apr 05, 2025
-
What Is A Push Or A Pull
Apr 05, 2025
-
Greatest Common Multiple Of 9 And 15
Apr 05, 2025
-
70 As A Fraction In Simplest Form
Apr 05, 2025
-
What Is 1 3 Of 1
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 7/9 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
