What Is 1 3 Of 1
listenit
Apr 05, 2025 · 5 min read
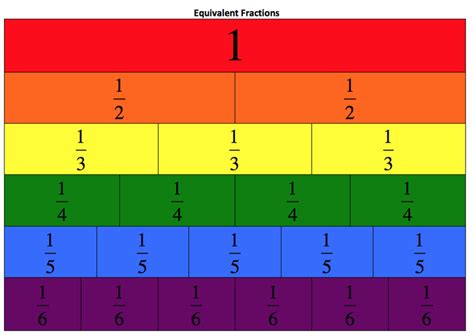
Table of Contents
What is 1/3 of 1? A Deep Dive into Fractions and Their Applications
The seemingly simple question, "What is 1/3 of 1?" opens a door to a fascinating world of fractions, their practical applications, and their significance in various fields. While the answer might seem immediately obvious to some, a thorough exploration reveals the underlying mathematical concepts and the broad implications of understanding fractions.
Understanding Fractions: The Building Blocks of Mathematics
Before we delve into calculating 1/3 of 1, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In the fraction 1/3, the numerator is 1 and the denominator is 3. This means we're dealing with one part out of a total of three equal parts. Understanding this fundamental concept is crucial for grasping fractional calculations.
Calculating 1/3 of 1: A Step-by-Step Approach
To find 1/3 of 1, we simply multiply the fraction 1/3 by the whole number 1:
(1/3) * 1 = 1/3
The result is, unsurprisingly, 1/3. This highlights a fundamental property of fractions: any fraction multiplied by 1 remains unchanged. This seemingly straightforward calculation lays the groundwork for more complex fractional operations.
Expanding the Concept: Fractions in Real-World Applications
The concept of finding a fraction of a whole is not limited to abstract mathematical exercises. It has countless practical applications across numerous fields:
-
Cooking and Baking: Recipes often require fractional measurements. For example, a recipe might call for 1/3 cup of sugar or 2/3 of a teaspoon of salt. Understanding fractions is essential for accurate measurements and consistent results in culinary creations.
-
Construction and Engineering: Precision is paramount in construction and engineering projects. Fractions are used extensively in blueprints, measurements, and material calculations to ensure structural integrity and functionality. Imagine building a house without accurate fractional measurements – the outcome would be disastrous!
-
Finance and Economics: Fractions play a vital role in financial calculations, including interest rates, stock prices, and currency exchange rates. Understanding fractions is essential for making informed financial decisions. For example, calculating 1/3 of an investment’s return is a common practice for assessing performance.
-
Data Analysis and Statistics: Fractions are fundamental to statistical analysis and data representation. Data is often presented as fractions or percentages (which are essentially fractions expressed as parts of 100). Understanding fractions helps in interpreting data effectively and drawing meaningful conclusions.
-
Science and Technology: Many scientific concepts rely on fractional representations. For instance, in chemistry, the precise measurement of compounds often involves fractions of grams or milliliters. Similarly, in physics, calculating fractional changes in velocity or acceleration is common practice.
Beyond the Basics: More Complex Fractional Calculations
While calculating 1/3 of 1 is relatively simple, understanding fractions extends to more complex scenarios. Let's explore some related concepts:
-
Multiplying Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together. For instance, (1/3) * (2/5) = 2/15. This concept is crucial for many real-world calculations, such as finding a fraction of a fraction.
-
Adding and Subtracting Fractions: Adding and subtracting fractions requires finding a common denominator. This involves finding a number that is divisible by both denominators. For example, to add 1/3 and 1/2, we find the common denominator 6, resulting in (2/6) + (3/6) = 5/6. This skill is essential for numerous applications, from combining ingredients in a recipe to analyzing financial statements.
-
Dividing Fractions: Dividing fractions involves inverting the second fraction (switching the numerator and denominator) and then multiplying. For example, (1/3) / (2/5) = (1/3) * (5/2) = 5/6. This operation is useful in various scenarios, like determining the number of servings from a recipe based on fractional quantities.
-
Converting Fractions to Decimals and Percentages: Fractions can be easily converted to decimals by dividing the numerator by the denominator. 1/3, for example, is approximately 0.333... (a repeating decimal). Converting to a percentage involves multiplying the decimal by 100. Therefore, 1/3 is approximately 33.33%. This conversion is widely used in everyday contexts like expressing discounts or calculating tax rates.
The Significance of Fractions in Education
The importance of understanding fractions cannot be overstated, particularly in education. A solid grasp of fractions lays the foundation for more advanced mathematical concepts, including algebra, calculus, and geometry. Early exposure to fractions and their practical applications helps children develop critical thinking skills and problem-solving abilities.
Furthermore, inadequate understanding of fractions can hinder a student's progress in various subjects, including science, engineering, and economics. Therefore, providing effective and engaging instruction in fractions is crucial for ensuring students' success in their academic pursuits and future careers.
Exploring Further: Advanced Fractional Concepts
For those seeking a deeper understanding of fractions, several advanced concepts can be explored:
-
Rational Numbers: Fractions are a subset of rational numbers, which include all numbers that can be expressed as the ratio of two integers. Understanding rational numbers provides a broader perspective on the nature of fractions.
-
Irrational Numbers: In contrast to rational numbers, irrational numbers cannot be expressed as a ratio of two integers. Examples include π (pi) and the square root of 2. Understanding the distinction between rational and irrational numbers is crucial for a complete understanding of the number system.
-
Complex Fractions: Complex fractions involve fractions within fractions. They can be simplified by using various techniques, such as multiplying the numerator and denominator by the least common denominator.
Conclusion: The Ubiquity of Fractions
The seemingly simple question, "What is 1/3 of 1?" leads us down a path of discovery, revealing the profound importance of fractions in our daily lives and various fields of study. From cooking and baking to finance and engineering, fractions are indispensable tools for accurate measurement, calculation, and decision-making. Mastering fractions is not merely an academic exercise; it is a fundamental skill that empowers individuals to navigate the complexities of the world around them with greater understanding and precision. The next time you encounter a fractional calculation, remember the significance of this seemingly simple concept and appreciate its widespread influence on our lives.
Latest Posts
Latest Posts
-
How Many Ounces Are In A Fifth Of Whiskey
Apr 05, 2025
-
Which Element Has Chemical Properties Most Similar To Sodium
Apr 05, 2025
-
What Shape Has 4 Right Angles
Apr 05, 2025
-
Dna Replication Is Said To Be Semiconservative Because
Apr 05, 2025
-
Why Is A Graduated Cylinder More Accurate Than A Beaker
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
