What Is 60 Percent Of 40
listenit
Apr 05, 2025 · 5 min read
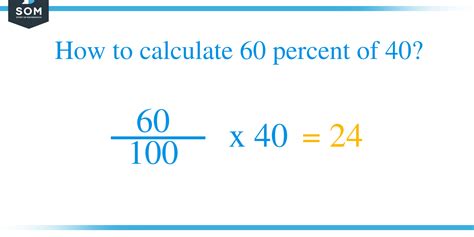
Table of Contents
What is 60 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 60 percent of 40 might seem like a simple calculation, but it opens a door to understanding a fundamental concept in mathematics with widespread applications in various fields. This article will not only answer the question directly but also explore the underlying principles of percentage calculations, different methods for solving such problems, and real-world examples showcasing the practical relevance of percentages.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." For instance, 60% means 60 out of 100, or 60/100. This fraction can be simplified to 3/5, illustrating the interconnectedness of percentages, fractions, and decimals.
The Importance of Percentages
Percentages are ubiquitous in our daily lives. We encounter them in:
- Finance: Interest rates on loans and savings accounts, discounts on purchases, tax calculations, investment returns, and inflation rates are all expressed as percentages.
- Retail: Sales, discounts, and markups are frequently represented using percentages to attract customers and calculate profits.
- Statistics: Data analysis, surveys, and polls often present findings as percentages to summarize and compare information effectively.
- Science: Scientific data and experimental results are often expressed as percentages to illustrate the magnitude of changes or effects.
- Education: Grades, test scores, and performance evaluations often use percentages to quantify achievement.
Understanding percentages is crucial for informed decision-making in numerous contexts. Whether it's evaluating a financial offer, understanding survey results, or interpreting scientific findings, a solid grasp of percentage calculations is essential.
Calculating 60% of 40: Three Methods
Now, let's tackle the core question: what is 60% of 40? We can employ several methods to arrive at the correct answer.
Method 1: Using the Fraction Method
This method involves converting the percentage to a fraction and then multiplying it by the given number.
- Convert the percentage to a fraction: 60% = 60/100
- Simplify the fraction: 60/100 simplifies to 3/5.
- Multiply the fraction by the number: (3/5) * 40 = 24
Therefore, 60% of 40 is 24.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying it by the given number.
- Convert the percentage to a decimal: 60% = 0.60 (or simply 0.6)
- Multiply the decimal by the number: 0.6 * 40 = 24
Again, we arrive at the answer: 60% of 40 is 24.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion:
- x/40 = 60/100
Where 'x' represents the unknown value (60% of 40). To solve for x, we cross-multiply:
- 100x = 60 * 40
- 100x = 2400
- x = 2400/100
- x = 24
This confirms that 60% of 40 is indeed 24.
Advanced Percentage Calculations and Applications
While calculating 60% of 40 is straightforward, let's explore more complex scenarios to further solidify our understanding of percentages.
Finding the Percentage: Reverse Calculations
Sometimes, you might know the result and one of the numbers, and need to find the percentage. For example, if 24 is 60% of a number, what is that number?
We can set up a proportion:
- 24/x = 60/100
Cross-multiplying and solving for 'x':
- 60x = 2400
- x = 40
This confirms our original problem.
Percentage Increase and Decrease
Percentages are essential for calculating increases or decreases. Imagine a product initially priced at $40 experiences a 20% price increase. The calculation would be:
- Calculate the increase: 20% of $40 = 0.20 * $40 = $8
- Add the increase to the original price: $40 + $8 = $48
The new price after a 20% increase is $48. Similarly, a 15% decrease would be calculated by finding 15% of $40 and subtracting it from the original price.
Compound Percentage Changes
Compound percentage changes involve applying a percentage change multiple times. For instance, if a $40 investment grows by 10% per year for two years, the calculation involves applying the 10% increase twice:
- Year 1: $40 * 0.10 = $4 increase; $40 + $4 = $44
- Year 2: $44 * 0.10 = $4.40 increase; $44 + $4.40 = $48.40
The final value after two years of 10% compound growth is $48.40. Note that this is different from a single 20% increase.
Percentage Points vs. Percentage Change
It's crucial to distinguish between percentage points and percentage change. A change from 40% to 60% is a 20 percentage point increase, but it represents a 50% increase relative to the original 40%.
Real-world Applications of Percentage Calculations
The applications of percentage calculations are vast and diverse. Here are a few examples:
- Calculating Sales Tax: If the sales tax in your area is 6%, and you buy an item for $100, the sales tax would be $6 (6% of $100), resulting in a total cost of $106.
- Determining Discounts: A 25% discount on a $50 item means the discount is $12.50 (25% of $50), leading to a final price of $37.50.
- Understanding Interest Rates: If you have a savings account with a 3% annual interest rate and a balance of $1,000, you would earn $30 in interest ($3% of $1,000) after one year.
- Analyzing Survey Results: If 70% of respondents in a survey favor a particular policy, this signifies strong public support for that policy.
- Interpreting Statistical Data: Many statistical measures like growth rates, unemployment rates, and inflation rates are expressed as percentages.
Conclusion
The simple calculation of 60% of 40 – which is 24 – serves as a gateway to understanding the significance and widespread applications of percentages in diverse fields. Mastering percentage calculations is crucial for effective decision-making in personal finance, business, statistics, and numerous other areas. By understanding the different methods for calculating percentages and their applications, you can confidently navigate numerical problems and interpret data in a meaningful way. Remember the core concepts – percentages as fractions of 100, the various calculation methods, and the distinction between percentage points and percentage changes – to build a strong foundation in this fundamental mathematical skill. The ability to confidently handle percentages will significantly enhance your analytical abilities and provide a valuable tool for understanding the world around you.
Latest Posts
Latest Posts
-
Is Square Root Of 4 A Rational Number
Apr 06, 2025
-
Why Is The Light Microscope Also Called The Compound Microscope
Apr 06, 2025
-
What Is 15 4 As A Mixed Number
Apr 06, 2025
-
Sublimation Is Physical Or Chemical Change
Apr 06, 2025
-
Write 2 1 2 As An Improper Fraction
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
