What Is 3.6 In A Fraction
listenit
Apr 01, 2025 · 4 min read
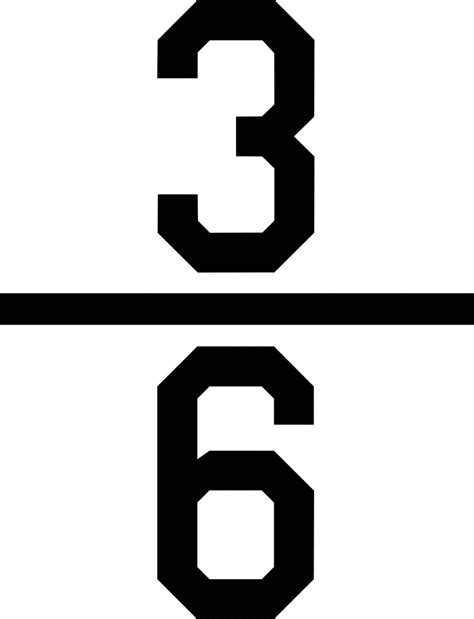
Table of Contents
What is 3.6 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the decimal 3.6 into its fractional equivalent, exploring various methods and providing a detailed explanation for a complete understanding. We'll also touch upon the importance of simplifying fractions and explore related concepts to solidify your knowledge.
Understanding Decimals and Fractions
Before we jump into converting 3.6, let's briefly revisit the concepts of decimals and fractions.
Decimals: Decimals represent parts of a whole number using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, in the decimal 3.6, the "3" represents three whole units, and the ".6" represents six-tenths.
Fractions: Fractions represent parts of a whole number using a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For example, ½ represents one part out of two equal parts.
Converting 3.6 to a Fraction: The Step-by-Step Approach
The key to converting decimals to fractions lies in understanding the place value of the decimal digits. Here’s how we convert 3.6:
-
Identify the Decimal Part: The decimal part of 3.6 is 0.6. This represents six-tenths.
-
Write it as a Fraction: We can write this decimal part as a fraction: ⁶⁄₁₀. The numerator (6) represents the digits after the decimal point, and the denominator (10) represents the place value of the last digit (tenths).
-
Combine with the Whole Number: We now have the fractional representation of the decimal part. We need to add the whole number part (3) to this fraction. We can do this by expressing the whole number as an improper fraction:
3 can be written as ³⁰⁄₁₀ (because 3 x 10 =30).
-
Add the Fractions: Now we add the two fractions: ³⁰⁄₁₀ + ⁶⁄₁₀ = ³⁶⁄₁₀
-
Simplify the Fraction (If Possible): We can simplify this fraction by finding the greatest common divisor (GCD) of the numerator (36) and the denominator (10). The GCD of 36 and 10 is 2. Dividing both the numerator and the denominator by 2, we get:
³⁶⁄₁₀ = ¹⁸⁄₅
Therefore, 3.6 as a fraction is ¹⁸⁄₅. This is an improper fraction because the numerator (18) is greater than the denominator (5).
Alternative Method: Using Place Value Directly
Another method to convert 3.6 into a fraction involves directly considering the place value of the digits:
-
Read the decimal: 3.6 is read as "three and six-tenths".
-
Write the fractional part: "six-tenths" translates directly to the fraction ⁶⁄₁₀.
-
Combine with the whole number: "Three and six-tenths" becomes 3 + ⁶⁄₁₀.
-
Convert the whole number to a fraction: 3 can be written as ³⁰⁄₁₀.
-
Add the fractions: ³⁰⁄₁₀ + ⁶⁄₁₀ = ³⁶⁄₁₀.
-
Simplify: Again, simplifying ³⁶⁄₁₀ by dividing both the numerator and denominator by their GCD (2) yields ¹⁸⁄₅.
Both methods lead to the same simplified improper fraction: ¹⁸⁄₅.
Converting Improper Fractions to Mixed Numbers
An improper fraction (where the numerator is larger than the denominator) can be converted into a mixed number (a whole number and a proper fraction). Let's convert ¹⁸⁄₅ into a mixed number:
-
Divide the numerator by the denominator: 18 ÷ 5 = 3 with a remainder of 3.
-
The whole number part: The quotient (3) becomes the whole number part of the mixed number.
-
The fractional part: The remainder (3) becomes the numerator of the fraction, and the original denominator (5) remains the denominator.
Therefore, ¹⁸⁄₅ as a mixed number is 3 ³⁄₅. Notice that this confirms our initial understanding of 3.6, where "3" represents the whole number and ".6" represents six-tenths (³⁄₅).
Importance of Simplifying Fractions
Simplifying fractions is crucial for several reasons:
-
Clarity: Simplified fractions are easier to understand and work with. ¹⁸⁄₅ is less intuitive than 3 ³⁄₅, particularly in practical applications.
-
Standard Form: In mathematics, simplified fractions are considered the standard form for representing rational numbers.
-
Comparison: Simplifying allows for easier comparison between fractions.
-
Calculations: Simplified fractions simplify subsequent calculations involving the fraction.
Practicing Decimal to Fraction Conversions
Converting decimals to fractions is a skill that improves with practice. Here are a few more examples to reinforce your understanding:
- 2.5: 2.5 = ²⁵⁄₁₀ = ⁵⁄₂ = 2 ½
- 0.75: 0.75 = ⁷⁵⁄₁₀₀ = ³⁄₄
- 1.25: 1.25 = ¹²⁵⁄₁₀₀ = ⁵⁄₄ = 1 ¼
- 4.8: 4.8 = ⁴⁸⁄₁₀ = ²⁴⁄₅ = 4 ⁴⁄₅
Beyond 3.6: Handling More Complex Decimals
The methods described above can be applied to decimals with more digits after the decimal point. For example, to convert 3.625 to a fraction:
- Write it as ³⁶²⁵⁄₁₀₀₀
- Find the GCD of 3625 and 1000 (which is 25).
- Simplify by dividing both numerator and denominator by 25: ¹⁴⁵⁄₄₀ = ²⁹⁄₈ = 3 ⁵⁄₈
Conclusion
Converting decimals to fractions is a fundamental mathematical skill with widespread applications. By understanding the place value of decimal digits and the process of simplifying fractions, you can confidently convert any decimal to its fractional equivalent. Remember that practice is key to mastering this skill, and applying these methods to various decimal numbers will further enhance your understanding. The conversion of 3.6 to ¹⁸⁄₅ or 3 ³⁄₅ demonstrates a clear understanding of this fundamental concept. Now you're well-equipped to tackle more complex decimal-to-fraction conversions!
Latest Posts
Latest Posts
-
2x 3y 12 In Slope Intercept Form
Apr 02, 2025
-
How Many Valence Electrons Does Group 2 Have
Apr 02, 2025
-
Which Element Below Is Least Reactive
Apr 02, 2025
-
What Is C In An Exponential Inequality
Apr 02, 2025
-
What Is The Greatest Common Factor Of 28 And 35
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 3.6 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
