What Is 3/25 As A Percent
listenit
Mar 24, 2025 · 5 min read
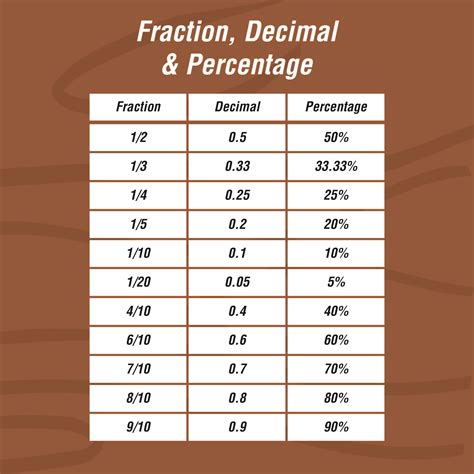
Table of Contents
What is 3/25 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts in shopping to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 3/25 into a percentage, explaining the underlying principles and providing various methods to solve similar problems. We'll also explore the broader context of fraction-to-percentage conversions, offering practical examples and tips to master this essential skill.
Understanding Fractions and Percentages
Before we tackle the conversion of 3/25, let's solidify our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/25, 3 is the numerator and 25 is the denominator.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent" or "out of 100". Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: Converting the Fraction to a Decimal
The most straightforward way to convert 3/25 to a percentage is by first converting it to a decimal. This involves dividing the numerator by the denominator:
3 ÷ 25 = 0.12
Now that we have the decimal equivalent (0.12), we can easily convert it to a percentage by multiplying by 100:
0.12 x 100 = 12%
Therefore, 3/25 is equal to 12%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction of 3/25 that has a denominator of 100. This is because percentages are essentially fractions with a denominator of 100. To achieve this, we need to determine what number we need to multiply the denominator (25) by to get 100.
25 x 4 = 100
Since we multiplied the denominator by 4, we must also multiply the numerator by the same factor to maintain the equivalence of the fraction:
3 x 4 = 12
This gives us the equivalent fraction 12/100, which directly translates to 12%.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the percentage. We can represent the problem as:
3/25 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
3 x 100 = 25 x x
300 = 25x
Now, divide both sides by 25:
x = 300 ÷ 25 = 12
Therefore, x = 12%, confirming that 3/25 is equal to 12%.
Practical Applications of Fraction-to-Percentage Conversions
Understanding fraction-to-percentage conversions is essential in various real-world scenarios:
- Sales and Discounts: If a store offers a 25% discount on an item, you can use this knowledge to calculate the actual saving.
- Financial Calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages.
- Data Analysis: Understanding percentages is vital when interpreting statistical data and charts, commonly used in business, science, and social studies.
- Cooking and Baking: Recipes often require adjusting ingredient quantities based on percentages.
- Everyday Life: Estimating tips, understanding tax rates, and comprehending various proportions all involve percentage calculations that originate from fraction conversions.
Advanced Concepts and Further Exploration
While converting 3/25 to a percentage is relatively simple, let's explore some more complex scenarios to solidify your understanding:
-
Converting Fractions Greater Than 1: If the fraction is an improper fraction (numerator greater than the denominator), the resulting percentage will be greater than 100%. For example, 5/2 = 2.5 = 250%.
-
Converting Mixed Numbers: A mixed number (whole number and a fraction) needs to be converted to an improper fraction before applying any of the conversion methods discussed above. For example, 2 1/4 is first converted to 9/4, then converted to a decimal (2.25) and finally to a percentage (225%).
-
Dealing with Recurring Decimals: Some fractions result in recurring decimals when converted. For example, 1/3 = 0.333... (recurring 3). In these cases, you can round the decimal to a certain number of decimal places before multiplying by 100 to get the percentage.
-
Using a Calculator: Calculators can significantly simplify the conversion process. Most calculators have a percentage function (%) that directly converts fractions (after dividing the numerator by the denominator) or decimals to percentages.
Troubleshooting Common Mistakes
Here are some common errors to avoid when converting fractions to percentages:
- Incorrect Division: Ensure you correctly divide the numerator by the denominator when converting to a decimal.
- Forgetting to Multiply by 100: Remember that the decimal needs to be multiplied by 100 to convert to a percentage.
- Confusing Numerator and Denominator: Always ensure you divide the numerator by the denominator, not the other way around.
Conclusion
Converting fractions to percentages is a crucial skill with practical applications in numerous fields. By understanding the various methods presented—converting to a decimal, finding equivalent fractions, and using proportions—you can confidently convert any fraction to a percentage. Remember to practice regularly and familiarize yourself with the common pitfalls to enhance your accuracy and speed. Mastering this skill will significantly improve your mathematical proficiency and your ability to tackle everyday percentage-based problems with ease. The simple conversion of 3/25 to 12% serves as a building block for a broader understanding of mathematical concepts and their real-world relevance.
Latest Posts
Latest Posts
-
65 Of What Number Is 26
Mar 27, 2025
-
What Percentage Is 6 Of 20
Mar 27, 2025
-
Sigma And Pi Bonds In Co2
Mar 27, 2025
-
Burning Wood Is A Chemical Change
Mar 27, 2025
-
The Most Abundant Gas In The Atmosphere
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
