What Is 1 3/4 Divided By 2 As A Fraction
listenit
May 24, 2025 · 5 min read
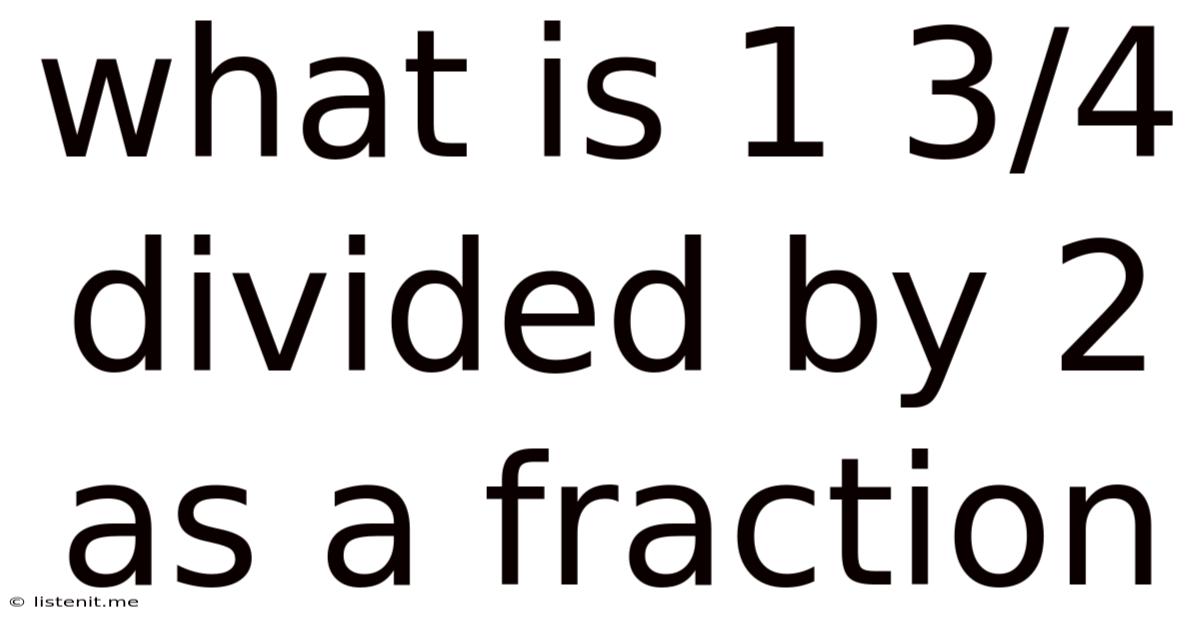
Table of Contents
What is 1 3/4 Divided by 2 as a Fraction? A Comprehensive Guide
Dividing fractions can seem daunting, especially when mixed numbers are involved. This comprehensive guide will walk you through the process of solving 1 3/4 divided by 2, explaining each step clearly and providing helpful tips and tricks for tackling similar problems. We'll not only find the answer but also delve into the underlying mathematical principles, ensuring a thorough understanding of the concept.
Understanding Fractions and Mixed Numbers
Before diving into the division, let's refresh our understanding of fractions and mixed numbers.
-
Fraction: A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator.
-
Mixed Number: A mixed number combines a whole number and a fraction. For example, 1 3/4 means one whole and three-quarters.
Converting Mixed Numbers to Improper Fractions
To divide fractions easily, it's best to convert mixed numbers into improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
To convert 1 3/4 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator: 4 + 3 = 7
- Keep the same denominator: 4
Therefore, 1 3/4 is equal to 7/4.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a simple yet powerful technique: finding the reciprocal and multiplying.
- Reciprocal: The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example, the reciprocal of 2/3 is 3/2. The reciprocal of a whole number, such as 2, is simply 1/2.
Let's apply this to our problem: 7/4 ÷ 2
-
Find the reciprocal of the divisor (2): The reciprocal of 2 is 1/2.
-
Change the division sign to a multiplication sign: 7/4 × 1/2
-
Multiply the numerators together: 7 * 1 = 7
-
Multiply the denominators together: 4 * 2 = 8
Therefore, 7/4 ÷ 2 = 7/8
Simplifying Fractions
Sometimes, the resulting fraction can be simplified. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
In our case, 7/8 is already in its simplest form because 7 and 8 have no common divisors other than 1.
Alternative Approach: Converting to Decimals
While the reciprocal method is generally preferred for fraction division, you can also solve this problem by converting the mixed number to a decimal and then dividing.
-
Convert 1 3/4 to a decimal: 1 3/4 = 1.75
-
Divide the decimal by 2: 1.75 ÷ 2 = 0.875
-
Convert the decimal back to a fraction: 0.875 can be expressed as 7/8 (This requires understanding decimal to fraction conversion).
This method confirms our previous result.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving math problems; it's a crucial skill with many real-world applications. Here are a few examples:
-
Cooking and Baking: Recipes often require dividing ingredients. For instance, if a recipe calls for 1 3/4 cups of flour but you want to halve the recipe, you'd need to calculate 1 3/4 cups ÷ 2.
-
Construction and Measurement: In construction, precise measurements are vital. Dividing lengths or quantities of materials frequently involves fractions.
-
Sewing and Crafts: Many craft projects require precise measurements and cutting of materials. Dividing lengths of fabric or yarn often involves fractions.
-
Data Analysis and Statistics: Working with datasets often requires calculating proportions and ratios, which frequently involves fraction division.
Troubleshooting Common Mistakes
When working with fractions, several common errors can occur. Let's address some of them:
-
Incorrect Reciprocal: Ensure you're correctly finding the reciprocal of the divisor. Remember to swap the numerator and denominator.
-
Multiplication Errors: Double-check your multiplication of the numerators and denominators. Even simple multiplication errors can lead to incorrect results.
-
Simplification Errors: Make sure you're simplifying the fraction to its lowest terms. If you don't simplify, the answer might be technically correct but not in its most concise form.
-
Mixing Methods: Avoid switching between methods mid-calculation. Stick to either the reciprocal method or the decimal conversion method for consistency.
Expanding Your Knowledge: Further Exploration of Fraction Operations
Understanding fraction division is a stepping stone to mastering other fraction operations. Here are some areas you can explore further:
-
Adding and Subtracting Fractions: Practice adding and subtracting fractions with different denominators. Learn about finding the least common denominator (LCD).
-
Multiplying Fractions: Review the process of multiplying fractions and simplifying the results.
-
Complex Fractions: Explore how to deal with fractions within fractions (complex fractions).
Conclusion: Mastering Fraction Division for Everyday Success
Mastering fraction division, particularly involving mixed numbers, is a valuable skill applicable to various aspects of life. By understanding the principles of reciprocals and practicing the steps outlined above, you'll confidently tackle fraction division problems and apply this knowledge to real-world situations. Remember to check for common errors and continue practicing to build your fluency and proficiency. The more you practice, the easier and more intuitive fraction operations will become. This will not only improve your mathematical skills but also enhance your problem-solving capabilities in diverse contexts.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 5 And 25
May 24, 2025
-
5 Out Of 20 Is What Percent
May 24, 2025
-
2 3 Divided By 5 6 In Fraction Form
May 24, 2025
-
How Many More Hours Till 7 Am
May 24, 2025
-
How Many Hours Is 8pm To 8am
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3/4 Divided By 2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.