2 3 Divided By 5 6 In Fraction Form
listenit
May 24, 2025 · 4 min read
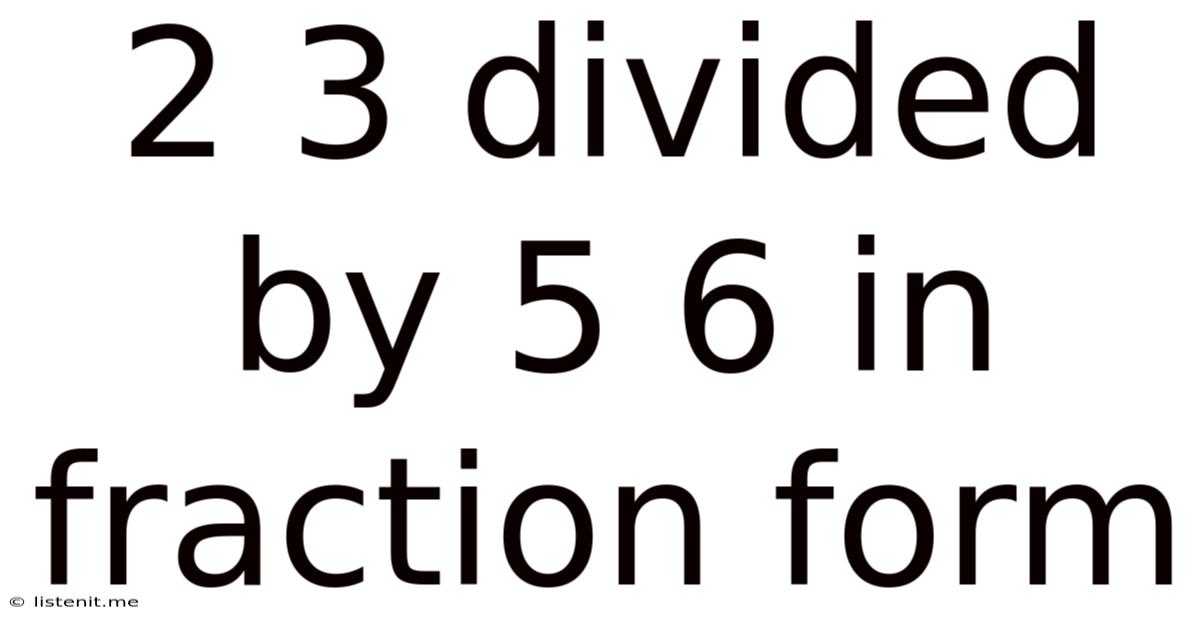
Table of Contents
Tackling the Fraction: 2/3 Divided by 5/6
Understanding how to divide fractions is a fundamental skill in mathematics, essential for various applications from baking to engineering. This comprehensive guide will walk you through the process of dividing 2/3 by 5/6, explaining the concepts in detail and offering practical tips to improve your fraction manipulation skills. We'll delve into the 'why' behind the method, not just the 'how', ensuring a solid grasp of the underlying principles.
Understanding Fraction Division: The "Invert and Multiply" Rule
The seemingly complex operation of dividing fractions simplifies significantly with a powerful technique: inverting the second fraction and multiplying. This isn't just a trick; it stems directly from the definition of division itself. Division asks, "How many times does one number fit into another?" When dealing with fractions, this translates to finding how many times 5/6 "fits into" 2/3.
Let's break down the "invert and multiply" rule:
1. The Reciprocal (Inverse): The reciprocal of a fraction is obtained by switching the numerator and denominator. For example, the reciprocal of 5/6 is 6/5. This represents the multiplicative inverse; when multiplied by the original fraction, the result is 1. (5/6 * 6/5 = 1)
2. Multiplication: Once you've inverted the second fraction, the division problem transforms into a multiplication problem. This makes the calculation significantly easier.
Step-by-Step Solution: 2/3 ÷ 5/6
Now, let's apply this rule to our problem: 2/3 ÷ 5/6.
Step 1: Invert the second fraction (the divisor):
The divisor is 5/6. Inverting it gives us 6/5.
Step 2: Change the division to multiplication:
Our problem now becomes: 2/3 * 6/5
Step 3: Multiply the numerators together and the denominators together:
Numerators: 2 * 6 = 12 Denominators: 3 * 5 = 15
This gives us the fraction: 12/15
Step 4: Simplify the fraction (if possible):
The fraction 12/15 can be simplified by finding the greatest common divisor (GCD) of 12 and 15. The GCD of 12 and 15 is 3. Dividing both the numerator and denominator by 3 simplifies the fraction:
12 ÷ 3 = 4 15 ÷ 3 = 5
Therefore, the simplified answer is 4/5.
Visualizing Fraction Division
Visual representations can be incredibly helpful in understanding fraction division. Imagine you have a pizza cut into thirds (representing 2/3). You want to divide this into portions of 5/6. How many 5/6 slices fit into the 2/3? This is precisely what the division problem represents. While a perfect visual representation for this specific division might be complex to draw precisely, the concept clarifies the meaning of the operation.
Practical Applications of Fraction Division
Fraction division is not merely an abstract mathematical concept; it's integral to various real-world applications:
-
Cooking and Baking: Recipes often require adjusting ingredient quantities. If a recipe calls for 2/3 cup of flour and you want to make only half the recipe, you'll need to divide 2/3 by 2 (or multiply by 1/2).
-
Construction and Engineering: Dividing fractions is crucial for precise measurements and calculations in construction projects, ensuring accurate dimensions and material usage.
-
Sewing and Fabric Design: Calculating fabric requirements for clothing or other textile projects frequently involves dividing fractions to account for seams, patterns, and other design elements.
-
Finance and Budgeting: When dealing with percentages and proportions of budgets, dividing fractions becomes indispensable for accurate financial planning.
Beyond the Basics: More Complex Fraction Division Problems
While 2/3 ÷ 5/6 is a relatively straightforward example, the principles remain the same for more intricate problems involving mixed numbers or larger fractions.
Mixed Numbers: A mixed number is a combination of a whole number and a fraction (e.g., 1 1/2). To divide with mixed numbers, first convert them into improper fractions (where the numerator is larger than the denominator). For example, 1 1/2 becomes 3/2. Then, apply the "invert and multiply" rule as described above.
Large Fractions: Dealing with fractions with larger numerators and denominators might initially seem daunting, but the process remains identical. Always simplify the resulting fraction to its lowest terms for clarity and ease of interpretation.
Mastering Fraction Division: Tips and Practice
Consistent practice is key to mastering fraction division. Here are some tips to improve your skills:
-
Start with simpler problems: Begin with easy fraction division problems to build confidence and familiarity with the method.
-
Practice regularly: Consistent practice solidifies your understanding and improves your speed and accuracy.
-
Use visual aids: Diagrams and visual representations can help grasp the concepts more intuitively.
-
Check your work: Always verify your answers to ensure accuracy.
-
Seek help when needed: Don't hesitate to consult textbooks, online resources, or tutors if you encounter difficulties.
Conclusion: Conquering Fraction Division
Dividing fractions might appear challenging at first, but understanding the "invert and multiply" rule and practicing regularly makes it a manageable and even enjoyable skill. This comprehensive guide has provided a step-by-step approach to solve 2/3 ÷ 5/6, highlighted real-world applications, and offered valuable tips for mastering this essential mathematical concept. By applying these strategies, you'll build a solid foundation in fraction arithmetic, paving the way for success in more advanced mathematical endeavors. Remember, consistent practice is the key to unlocking your full potential in mathematics.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 18 And 81
May 24, 2025
-
If I Was Born 1965 How Old Am I
May 24, 2025
-
How Long Is 5 Years In Days
May 24, 2025
-
Calories Burned Calculator By Heart Rate
May 24, 2025
-
Convert Z Score To Raw Score
May 24, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 5 6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.