5 Out Of 20 Is What Percent
listenit
May 24, 2025 · 4 min read
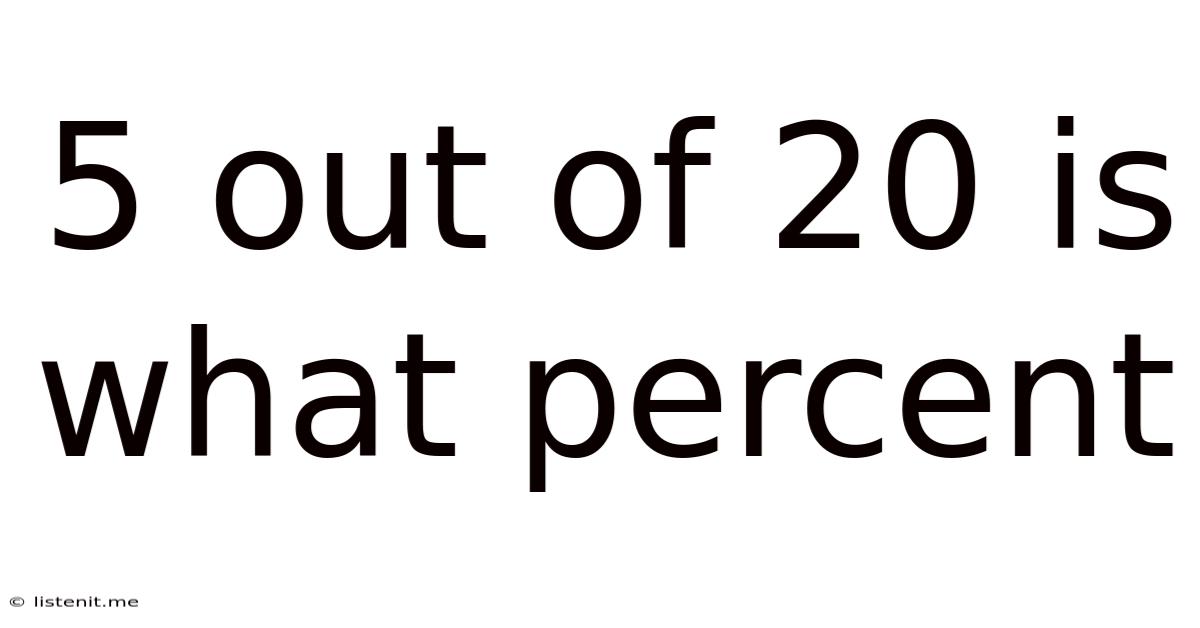
Table of Contents
5 Out of 20 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many areas of life, from calculating discounts and taxes to understanding statistics and financial reports. Often, we encounter situations where we need to convert fractions or ratios into percentages. This article will comprehensively explore how to calculate percentages, focusing specifically on the question: "5 out of 20 is what percent?" We'll delve into the process, offer different methods, and provide practical applications to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, a percentage represents a proportion out of a total of 100 parts. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Method 1: Using the Formula
The most straightforward way to calculate a percentage is using a simple formula:
(Part / Whole) * 100 = Percentage
In our example, "5 out of 20," 5 represents the part, and 20 represents the whole. Let's plug these values into the formula:
(5 / 20) * 100 = 25%
Therefore, 5 out of 20 is 25%.
Method 2: Simplifying the Fraction
Before applying the formula, we can simplify the fraction 5/20. Both the numerator (5) and the denominator (20) are divisible by 5:
5 / 20 = 1 / 4
Now, we can convert the simplified fraction 1/4 to a percentage:
(1 / 4) * 100 = 25%
This method demonstrates that simplifying the fraction first can often make the calculation easier.
Method 3: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first and then multiplying by 100:
5 / 20 = 0.25
0.25 * 100 = 25%
This method highlights the direct relationship between decimals and percentages. Multiplying a decimal by 100 moves the decimal point two places to the right.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios:
1. Sales and Discounts:
Imagine a store offers a 25% discount on an item. If the original price is $80, you can calculate the discount amount using the percentage:
$80 * 0.25 = $20
The discount is $20, and the final price is $80 - $20 = $60.
2. Taxes and Tips:
Calculating sales tax or service tips often involves percentages. If the tax rate is 6% on a $50 meal, the tax amount is:
$50 * 0.06 = $3
The total cost, including tax, is $50 + $3 = $53.
3. Grade Calculation:
In education, percentages are used to represent grades. If you answered 15 out of 20 questions correctly on a test, your percentage score is:
(15 / 20) * 100 = 75%
4. Financial Analysis:
Percentage changes are frequently used in finance to track growth or decline in investments, profits, or expenses. For example, if a company's profits increased from $100,000 to $125,000, the percentage increase is:
(($125,000 - $100,000) / $100,000) * 100 = 25%
Beyond the Basics: More Complex Percentage Problems
While calculating "5 out of 20" is straightforward, percentage problems can become more complex. Let's explore some variations:
1. Finding the Whole:
Suppose you know that 25% of a number is 15. To find the whole number, you can set up an equation:
0.25 * x = 15
Solving for x:
x = 15 / 0.25 = 60
Therefore, the whole number is 60.
2. Finding the Part:
If you know the whole and the percentage, you can find the part. For example, what is 30% of 80?
80 * 0.30 = 24
The part is 24.
3. Percentage Increase or Decrease:
Calculating percentage changes requires understanding the difference between the initial and final values. For example, if a value increases from 50 to 75, the percentage increase is:
((75 - 50) / 50) * 100 = 50%
Similarly, if a value decreases from 100 to 80, the percentage decrease is:
((100 - 80) / 100) * 100 = 20%
Mastering Percentages: Tips and Tricks
-
Practice regularly: The best way to master percentage calculations is through consistent practice. Solve various problems to build your confidence and understanding.
-
Use a calculator: For more complex calculations, utilize a calculator to ensure accuracy.
-
Understand the context: Pay close attention to the wording of problems to correctly identify the part and the whole.
-
Check your work: Always review your answers to ensure they make logical sense within the context of the problem.
-
Visual aids: Consider using visual aids like pie charts or bar graphs to represent percentages and improve your comprehension.
Conclusion: The Power of Percentage Understanding
Understanding percentages is a valuable skill applicable across numerous fields. Whether you're calculating discounts, analyzing financial data, or assessing grades, mastering percentage calculations enhances your ability to interpret information effectively and make informed decisions. The seemingly simple question, "5 out of 20 is what percent?", serves as a gateway to a broader understanding of this fundamental mathematical concept, empowering you to navigate various numerical challenges with confidence. Remember to practice regularly, utilize different methods, and always check your work for accuracy. The more you practice, the more comfortable and proficient you will become in solving percentage problems.
Latest Posts
Latest Posts
-
How Many Seconds Are In 3 5 Hours
May 24, 2025
-
What Is The Gcf Of 8 And 5
May 24, 2025
-
Greatest Common Factor Of 3 And 12
May 24, 2025
-
What Was The Date Of Last Friday
May 24, 2025
-
Find The Greatest Common Factor Of 16 27 And 20
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 20 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.