What Does All Rhombuses Have In Common
listenit
Mar 31, 2025 · 5 min read
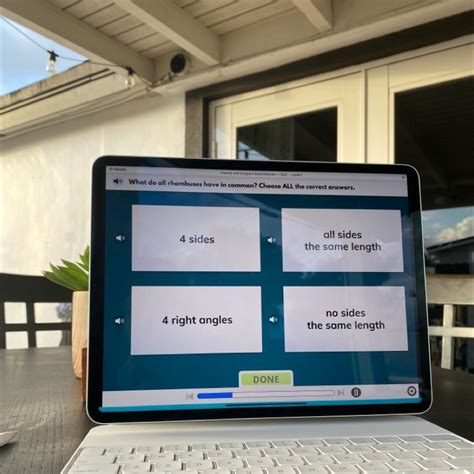
Table of Contents
What Do All Rhombuses Have in Common? A Comprehensive Exploration
Rhombuses. The very word conjures images of slanted squares, diamond shapes, and perhaps even a certain playing card. But beyond their visual similarities, what truly unites all rhombuses? This comprehensive exploration delves deep into the geometric properties of rhombuses, revealing the common threads that bind these fascinating quadrilaterals together. We’ll examine their sides, angles, diagonals, area calculation, and even their relationship to other quadrilaterals, ensuring a complete and SEO-optimized understanding.
Defining the Rhombus: A Foundation of Shared Characteristics
Before we delve into the specifics, let's establish a clear definition: a rhombus is a quadrilateral (a four-sided polygon) where all four sides are of equal length. This fundamental property is the cornerstone upon which all other characteristics of a rhombus are built. It's the sine qua non, the essential defining feature. Without equal sides, a shape simply isn't a rhombus.
Beyond Equal Sides: Exploring Other Shared Properties
While equal sides are the defining characteristic, several other properties are inherently linked and shared by all rhombuses:
1. Opposite Sides are Parallel:
This property stems directly from the equal side lengths. Because the opposite sides are equal in length and connected by parallel lines, they automatically become parallel to each other. This makes a rhombus a special type of parallelogram. This parallel characteristic is crucial for understanding other geometric relationships within the rhombus.
2. Opposite Angles are Equal:
Similar to the parallel sides, the opposite angles within a rhombus are always equal. This is a direct consequence of the figure’s parallel sides and the properties of parallelograms. If you draw two lines intersecting each other, the opposite angles created are always equal, and this principle applies directly to the rhombus.
3. Consecutive Angles are Supplementary:
Consecutive angles (angles next to each other) in a rhombus always add up to 180 degrees. This is another inherent property flowing from the parallelogram characteristic. This supplementary angle relationship is essential when working with angle calculations and problem-solving within the rhombus.
4. Diagonals Bisect Each Other:
The diagonals of a rhombus (the lines connecting opposite corners) always intersect at a right angle, and importantly, they bisect each other – meaning they cut each other exactly in half. This is a key characteristic that differentiates it from other quadrilaterals. This property is crucial for various geometric calculations and constructions.
5. Diagonals Bisect the Angles:
The diagonals of a rhombus not only bisect each other but also bisect the angles of the rhombus. This means each diagonal splits its corresponding angles into two equal halves. This angle-bisecting property is a powerful tool for solving problems related to angles and symmetries within the rhombus.
Rhombuses and Other Quadrilaterals: The Family Connections
Understanding the relationships between a rhombus and other quadrilaterals provides a deeper appreciation of its unique place in geometry:
-
Parallelogram: A rhombus is a special type of parallelogram. All rhombuses are parallelograms, but not all parallelograms are rhombuses. The key difference lies in the equal side length requirement.
-
Rectangle: A rhombus can be a rectangle (and vice versa) if and only if all its angles are right angles (90 degrees). In this specific case, the rhombus becomes a square.
-
Square: A square is a rhombus with all angles equal to 90 degrees. It's the most symmetrical type of rhombus.
-
Kite: A rhombus shares some similarities with a kite (two pairs of adjacent sides are equal), but the key difference is that a kite does not necessarily have parallel opposite sides.
Calculating the Area of a Rhombus: Methods and Applications
Determining the area of a rhombus involves several methods, each leveraging its unique geometric properties:
Method 1: Using Base and Height
Like other parallelograms, the area of a rhombus can be calculated using the formula: Area = base × height. Here, the 'base' is the length of any side, and the 'height' is the perpendicular distance between that side and its opposite parallel side.
Method 2: Using Diagonals
A more elegant and often more practical method utilizes the diagonals. The area of a rhombus can also be calculated using the formula: Area = (1/2) × d1 × d2, where d1 and d2 are the lengths of the two diagonals. This method eliminates the need to find the height, making it especially useful in many practical scenarios.
Real-World Applications of Rhombuses
Rhombuses, while seemingly abstract geometric shapes, find numerous applications in the real world:
-
Engineering and Design: Rhombus shapes are used in structural designs to provide strength and stability, appearing in bridges, buildings, and other structures.
-
Art and Design: Their symmetrical and visually appealing nature makes them a common feature in art, design, and decorative patterns.
-
Nature: Certain crystal structures and natural formations exhibit rhombus-like shapes.
-
Games: Playing cards and various games utilize rhombus shapes in their design.
Beyond the Basics: Advanced Concepts and Exploration
For those seeking a more in-depth understanding, let's explore some advanced concepts related to rhombuses:
1. Rhombus in Coordinate Geometry:
Representing and analyzing rhombuses using coordinate geometry allows for precise calculations and a deeper understanding of their properties using algebraic equations.
2. Transformations of Rhombuses:
Exploring how transformations like rotations, reflections, and translations affect rhombuses provides insights into their symmetries and properties.
3. Rhombuses in Higher Dimensions:
The concept of a rhombus can be extended to higher dimensions, providing a fascinating glimpse into abstract geometry.
Conclusion: A Deeper Appreciation of the Rhombus
This exploration has uncovered the fundamental properties shared by all rhombuses: equal sides, opposite sides parallel, opposite angles equal, consecutive angles supplementary, and unique diagonal properties. Understanding these characteristics not only enhances geometric knowledge but also opens doors to practical applications across various fields. The rhombus, seemingly simple at first glance, proves to be a rich source of mathematical exploration and real-world relevance. Its multifaceted nature, intertwined with other quadrilaterals, showcases the elegance and interconnectedness within the world of geometry. From its basic definition to advanced applications, the rhombus remains a compelling subject for study and discovery.
Latest Posts
Latest Posts
-
How Does Igneous Rock Become Metamorphic
Apr 01, 2025
-
How Does Friction Affect The Motion Of Objects
Apr 01, 2025
-
Sr Oh 2 Strong Or Weak
Apr 01, 2025
-
A Bond In Which Electrons Are Shared Unequally
Apr 01, 2025
-
Greatest Common Factor Of 32 And 36
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Does All Rhombuses Have In Common . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
