The Fourth Root Of 16 Is
listenit
Apr 01, 2025 · 6 min read
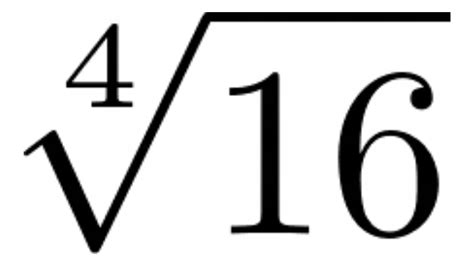
Table of Contents
- The Fourth Root Of 16 Is
- Table of Contents
- The Fourth Root of 16: Unveiling the Mathematical Mystery and its Broader Implications
- Understanding Roots and Radicals
- Calculating the Fourth Root of 16
- Exploring the Concept of Multiple Roots
- Connecting to Complex Numbers
- Applications of Roots and Radicals
- Advanced Concepts and Further Exploration
- Conclusion: Beyond the Simple Answer
- Latest Posts
- Latest Posts
- Related Post
The Fourth Root of 16: Unveiling the Mathematical Mystery and its Broader Implications
The seemingly simple question, "What is the fourth root of 16?", opens a door to a fascinating exploration of mathematics, encompassing fundamental concepts and their far-reaching applications. While the answer itself is straightforward (2), the journey to understanding it and its implications reveals a rich tapestry of mathematical ideas. This article will delve deep into this seemingly simple problem, exploring its solution, its connection to other mathematical concepts, and its applications in various fields.
Understanding Roots and Radicals
Before we tackle the fourth root of 16, let's solidify our understanding of roots and radicals. A root is the inverse operation of exponentiation. For example, if we have the equation x² = 9, finding the square root of 9 gives us the value of x (which is ±3). The notation for a root is a radical symbol (√), where the number inside the radical is called the radicand, and the small number above the radical (called the index) indicates the type of root.
- Square root (index 2): √x (often written without the index 2)
- Cube root (index 3): ³√x
- Fourth root (index 4): ⁴√x
- nth root (index n): ⁿ√x
The nth root of a number 'x' is a value 'a' such that aⁿ = x. This means that if we raise 'a' to the power of 'n', we get 'x'.
Calculating the Fourth Root of 16
Now, let's address the question at hand: What is the fourth root of 16? We are looking for a number that, when multiplied by itself four times, equals 16. In mathematical notation, this is represented as:
⁴√16 = x
This means x⁴ = 16. By trial and error, or by recognizing that 2 x 2 x 2 x 2 = 16, we arrive at the solution:
x = 2
Therefore, the fourth root of 16 is 2. However, the story doesn't end there. The concept of roots, especially with even indices, introduces the possibility of negative solutions.
Exploring the Concept of Multiple Roots
Unlike odd-indexed roots, even-indexed roots (like the square root, fourth root, sixth root, etc.) can have both positive and negative solutions. This is because a negative number raised to an even power results in a positive number. For example:
(-2)⁴ = (-2) x (-2) x (-2) x (-2) = 16
This means that -2 is also a fourth root of 16. However, in most basic mathematical contexts, we often focus on the principal root, which is the non-negative solution. Thus, while both 2 and -2 are fourth roots of 16, 2 is often considered the principal fourth root.
Connecting to Complex Numbers
The concept of roots becomes significantly more intricate when dealing with negative radicands and even indices. For instance, consider the square root of -1. There's no real number that, when multiplied by itself, results in -1. This is where complex numbers come into play. Complex numbers are numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, defined as the square root of -1 (i² = -1).
Complex numbers allow us to extend the concept of roots to include negative radicands. While the fourth root of 16 has real solutions (2 and -2), consider the fourth root of -16. This introduces complex solutions that involve the imaginary unit 'i'. Understanding these complex solutions requires a deeper dive into complex number arithmetic and the polar form of complex numbers.
Applications of Roots and Radicals
The seemingly simple operation of finding the fourth root of 16, and more generally, calculating roots, finds numerous applications across various fields:
1. Geometry and Trigonometry:
Roots are crucial in geometrical calculations, especially when dealing with distances, areas, and volumes. For instance, calculating the diagonal of a square or the length of a hypotenuse in a right-angled triangle involves using the square root. Higher-order roots appear in more complex geometric problems and in trigonometric calculations.
2. Physics and Engineering:
Root calculations are prevalent in physics and engineering, appearing in formulas related to:
- Velocity and acceleration: Many kinematic equations involve square roots and other higher-order roots.
- Energy calculations: Kinetic energy and other forms of energy often involve square roots in their equations.
- Signal processing: The root mean square (RMS) value, a crucial concept in signal processing, utilizes square roots to determine the effective value of an alternating current.
- Electrical Engineering: In electrical circuit analysis, impedance calculations often involve the square root of the sum of squares of resistance and reactance.
3. Financial Modeling:
Roots appear in financial models, particularly when dealing with:
- Compound interest calculations: Determining the present value or future value of an investment often involves using roots to account for the effects of compounding.
- Standard deviation in finance: In finance, standard deviation, a measure of risk, is calculated using square roots.
4. Computer Graphics and Game Development:
Roots are fundamental in computer graphics and game development:
- 3D transformations: Matrices and vectors used in 3D transformations frequently involve various root calculations.
- Lighting and shading algorithms: These algorithms often require calculating distances and other geometric properties, necessitating root operations.
5. Statistics and Data Analysis:
Roots play a vital role in statistical analysis:
- Standard deviation: As mentioned, standard deviation uses square roots.
- Root mean squared error (RMSE): This is a key metric in regression analysis, comparing observed values to predicted values.
Advanced Concepts and Further Exploration
The fourth root of 16, while seemingly simple, serves as a gateway to more advanced mathematical concepts. Here are some avenues for further exploration:
- Nth roots of unity: These are complex numbers that, when raised to the nth power, equal 1. Understanding these roots has applications in various areas like signal processing and Fourier analysis.
- Radical equations: These are equations where the variable appears under a radical symbol. Solving these equations requires specific techniques and often involves raising both sides to a power to eliminate the radical.
- Numerical methods for approximating roots: For many numbers, finding exact roots is impossible. Numerical methods, like the Newton-Raphson method, provide iterative approaches to approximate roots with high accuracy.
Conclusion: Beyond the Simple Answer
The seemingly straightforward question of "What is the fourth root of 16?" leads us on a journey that goes far beyond the simple answer of 2. It touches upon fundamental concepts like roots and radicals, introduces the intriguing world of complex numbers, and highlights the diverse applications of these mathematical ideas across numerous fields. Understanding this seemingly simple problem provides a strong foundation for tackling more complex mathematical challenges and appreciating the power and beauty of mathematics in our world. The exploration of roots reveals the interconnectedness of mathematical concepts and their practical significance, solidifying its importance in diverse scientific, engineering, and technological disciplines.
Latest Posts
Latest Posts
-
Where On The Periodic Table Are The Nonmetals Located
Apr 05, 2025
-
How Many Are In A Set
Apr 05, 2025
-
58333 As A Fraction Of An Inch
Apr 05, 2025
-
How Is A Mixture Different From A Compound
Apr 05, 2025
-
How Many Thirds Are In A Cup
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about The Fourth Root Of 16 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
