Sum Of Exterior Angles Of A Heptagon
listenit
Mar 28, 2025 · 6 min read
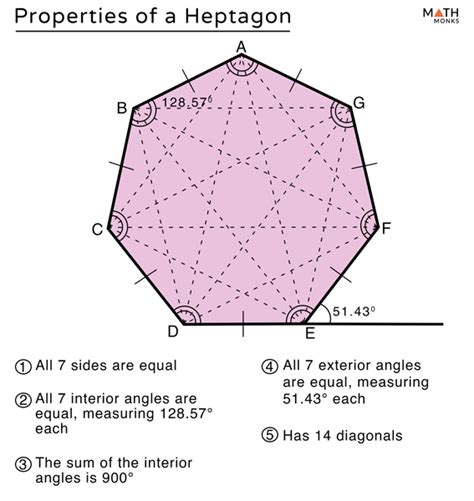
Table of Contents
The Sum of Exterior Angles of a Heptagon: A Comprehensive Exploration
The world of geometry is full of fascinating properties and relationships. One such captivating concept is the sum of the exterior angles of a polygon, a topic that holds significant importance in various mathematical applications. This article delves deep into understanding the sum of exterior angles, specifically focusing on a heptagon, a polygon with seven sides. We'll explore the concept from its fundamental principles to its practical applications, ensuring a thorough understanding for readers of all levels.
Understanding Polygons and Their Angles
Before diving into the specifics of a heptagon, let's establish a foundational understanding of polygons and their angles. A polygon is a closed two-dimensional figure composed of straight line segments. These segments are called sides, and the points where they meet are called vertices. Polygons are classified based on the number of sides they possess:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
And so on. Each polygon has both interior and exterior angles.
- Interior Angles: These are the angles formed inside the polygon by two adjacent sides.
- Exterior Angles: These are the angles formed between one side of the polygon and the extension of an adjacent side. For each interior angle, there is a corresponding exterior angle, and the two angles are supplementary (meaning their sum is 180 degrees).
Exploring the Heptagon
A heptagon, as mentioned earlier, is a polygon with seven sides and seven vertices. It can be regular (all sides and angles are equal) or irregular (sides and angles are of varying lengths and measures). Understanding the properties of its angles is crucial to comprehending its geometric characteristics.
Calculating the Sum of Interior Angles of a Heptagon
Before we tackle the exterior angles, let's briefly review calculating the sum of interior angles. A general formula exists for any polygon:
(n - 2) * 180°
Where 'n' is the number of sides of the polygon. For a heptagon (n = 7):
(7 - 2) * 180° = 5 * 180° = 900°
Therefore, the sum of the interior angles of any heptagon is always 900 degrees. This holds true whether the heptagon is regular or irregular.
Deriving the Sum of Exterior Angles of a Heptagon
Now, let's focus on the key topic: the sum of the exterior angles of a heptagon. Here's the crucial point: the sum of the exterior angles of any polygon is always 360 degrees. This remarkable property holds true regardless of the number of sides, whether the polygon is regular or irregular, concave or convex.
This can be intuitively understood by considering the exterior angles as the turns one makes while walking along the perimeter of the polygon. Starting at one vertex and moving along each side, you complete a full 360-degree rotation by the time you return to the starting point.
Therefore, the sum of the exterior angles of a heptagon, like any other polygon, is 360 degrees. This fundamental property is incredibly useful in various geometric proofs and problem-solving scenarios.
Proof of the Sum of Exterior Angles Theorem
While the intuitive explanation helps grasp the concept, a formal proof is essential for rigorous mathematical understanding. Let's consider a general polygon with 'n' sides:
-
Each interior angle and its corresponding exterior angle are supplementary. This means their sum is 180 degrees.
-
The sum of all interior angles of an n-sided polygon is (n - 2) * 180 degrees.
-
Let's represent the exterior angles as α₁, α₂, ..., αₙ.
-
The sum of an interior angle and its corresponding exterior angle is always 180 degrees. This can be represented as:
Interior Angle₁ + α₁ = 180° Interior Angle₂ + α₂ = 180° ... Interior Angleₙ + αₙ = 180°
-
Summing these equations, we get:
(Sum of Interior Angles) + (α₁ + α₂ + ... + αₙ) = 180°n
-
Substituting the formula for the sum of interior angles, we get:
(n - 2) * 180° + (α₁ + α₂ + ... + αₙ) = 180°n
-
Simplifying the equation, we find:
(α₁ + α₂ + ... + αₙ) = 180°n - (n - 2) * 180° = 360°
This proves that the sum of the exterior angles of any polygon, irrespective of the number of sides, is always 360 degrees.
Applications of the Sum of Exterior Angles Theorem
The seemingly simple property of the sum of exterior angles has far-reaching implications across various fields:
-
Cartography: Understanding polygon angles is crucial in mapmaking and geographic information systems (GIS) for accurate representation of landmasses and their boundaries.
-
Architecture and Engineering: Architects and engineers rely on geometric principles to design and construct stable and functional structures. Accurate angle calculations are essential for building bridges, skyscrapers, and other complex structures.
-
Computer Graphics: In computer graphics and game development, polygon manipulation is fundamental. The understanding of exterior angles aids in creating realistic and visually appealing 3D models and animations.
-
Robotics and Automation: Robotics often involves precise movements and positioning. Geometric calculations, including the properties of polygons and their angles, are essential for programming robots to perform tasks accurately.
-
Surveying and Land Measurement: Accurate land measurement relies on principles of geometry. Determining the area and boundaries of land parcels often involves calculations involving polygon angles.
Solving Problems Involving Heptagons
Let's consider some example problems involving heptagons to illustrate the application of the sum of exterior angles theorem:
Problem 1: A regular heptagon has seven equal exterior angles. Calculate the measure of each exterior angle.
Solution: Since the sum of the exterior angles of any polygon is 360°, and a regular heptagon has seven equal exterior angles, each exterior angle measures 360° / 7 ≈ 51.43°.
Problem 2: An irregular heptagon has six exterior angles measuring 40°, 50°, 60°, 70°, 80°, and 90°. Calculate the measure of the seventh exterior angle.
Solution: Let the seventh exterior angle be x. The sum of all seven exterior angles is 360°. Therefore:
40° + 50° + 60° + 70° + 80° + 90° + x = 360° 390° + x = 360° x = 360° - 390° = -30°
This negative result indicates an error in the problem statement or a concave heptagon (where at least one interior angle is greater than 180°).
Conclusion: The Significance of Understanding Polygons
The sum of exterior angles of a heptagon, and indeed of any polygon, is a fundamental concept in geometry with significant applications in diverse fields. Understanding this property, along with other geometric principles, provides a powerful toolkit for solving problems and tackling challenges across numerous disciplines. The 360-degree rule serves as a cornerstone of geometric understanding, underscoring the beauty and elegance of mathematical relationships. This consistent and predictable property enables us to analyze and manipulate polygons efficiently, contributing significantly to our understanding of shapes and spaces. Further exploration of polygon properties will undoubtedly reveal more fascinating intricacies within the world of geometry.
Latest Posts
Latest Posts
-
What Is 6 To The Zeroth Power
Mar 31, 2025
-
Which Intermolecular Force Is The Weakest
Mar 31, 2025
-
How To Calculate Molar Mass Of A Gas
Mar 31, 2025
-
The Weaker The Acid The Stronger The Conjugate Base
Mar 31, 2025
-
How Many Neutrons Does Barium Have
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Sum Of Exterior Angles Of A Heptagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
