Solve This Equation 4y 228 352
listenit
Apr 01, 2025 · 5 min read
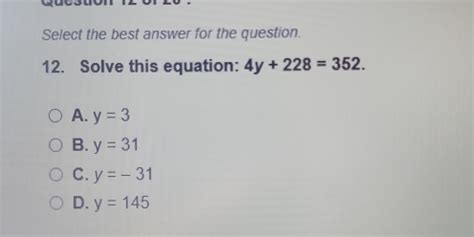
Table of Contents
Solving the Equation: 4y + 228 = 352 – A Step-by-Step Guide
This article provides a comprehensive guide on how to solve the algebraic equation 4y + 228 = 352. We'll break down the process step-by-step, explaining the underlying principles of algebra involved. We'll also explore different approaches to solving similar equations and discuss the importance of checking your solution. Finally, we'll touch upon the broader applications of solving linear equations in various fields.
Understanding the Equation
Before we dive into the solution, let's understand the components of the equation: 4y + 228 = 352.
- 4y: This represents a variable term. 'y' is an unknown value we aim to find, and '4' is its coefficient, indicating that 'y' is multiplied by 4.
- +228: This is a constant term added to the variable term.
- = 352: This indicates that the expression on the left-hand side (LHS) is equal to the expression on the right-hand side (RHS). 352 is a constant.
The goal is to isolate the variable 'y' to find its value. This involves manipulating the equation using algebraic principles, ensuring we maintain equality between the LHS and RHS at every step.
Solving the Equation: A Step-by-Step Approach
We will use the principles of inverse operations to isolate 'y'. Inverse operations are operations that undo each other; addition and subtraction are inverse operations, as are multiplication and division.
Step 1: Isolate the variable term.
To isolate the term with 'y' (4y), we need to eliminate the constant term (+228) from the LHS. We achieve this by subtracting 228 from both sides of the equation. This maintains the equality.
4y + 228 - 228 = 352 - 228
This simplifies to:
4y = 124
Step 2: Solve for the variable.
Now, 'y' is multiplied by 4. To isolate 'y', we perform the inverse operation of multiplication – division. We divide both sides of the equation by 4:
4y / 4 = 124 / 4
This simplifies to:
y = 31
Therefore, the solution to the equation 4y + 228 = 352 is y = 31.
Verifying the Solution
It's crucial to verify our solution by substituting the value of 'y' (31) back into the original equation:
4(31) + 228 = 352
124 + 228 = 352
352 = 352
Since the equation holds true, our solution (y = 31) is correct.
Alternative Approaches to Solving Linear Equations
While the above method is straightforward, there are other approaches to solving linear equations like this one. Let's briefly discuss some of them:
1. Using the Subtraction Property of Equality:
This property states that subtracting the same number from both sides of an equation maintains the equality. We already used this in Step 1 of our solution.
2. Using the Division Property of Equality:
This property states that dividing both sides of an equation by the same non-zero number maintains the equality. We used this in Step 2.
3. Graphical Method:
Although less practical for simple equations like this, the graphical method involves plotting the equation as a line on a coordinate plane. The x-intercept (where the line crosses the x-axis) represents the solution for x (in this case, y). This method is more useful for visualizing solutions and for solving systems of equations.
Applications of Solving Linear Equations
Solving linear equations is a fundamental skill in mathematics with far-reaching applications in various fields:
-
Science: Linear equations are used extensively in physics, chemistry, and biology to model relationships between variables. For example, calculating the velocity of an object, determining the concentration of a solution, or modeling population growth often involves solving linear equations.
-
Engineering: Engineers use linear equations to design structures, analyze circuits, and model systems. For example, calculating forces in a bridge, determining current flow in an electrical circuit, or simulating fluid flow often requires solving linear equations.
-
Economics: Economists use linear equations to model supply and demand, analyze market trends, and predict economic growth.
-
Finance: Financial analysts use linear equations to model investments, calculate returns, and analyze risk.
-
Computer Science: Linear equations play a critical role in computer graphics, computer vision, and machine learning algorithms.
-
Everyday Life: We unconsciously use linear equations in everyday life, for instance, when calculating the cost of items, determining the distance traveled, or converting units.
Expanding on Solving More Complex Equations
While the equation we solved was relatively straightforward, the principles applied can be extended to more complex linear equations. These might include:
-
Equations with fractions: For equations with fractions, the first step involves finding a common denominator to eliminate the fractions, simplifying the equation to a form similar to the one we solved.
-
Equations with decimals: Equations with decimals can be simplified by multiplying both sides by a power of 10 to eliminate the decimal points.
-
Equations with parentheses: Equations with parentheses require distributing terms before proceeding with the steps outlined above.
-
Equations with variables on both sides: For equations with variables on both sides, the first step is to combine like terms by adding or subtracting them to one side of the equation.
Mastering the fundamentals of solving simple linear equations, as demonstrated with 4y + 228 = 352, forms a strong foundation for tackling these more advanced equation types.
Conclusion
Solving the equation 4y + 228 = 352 involves applying fundamental algebraic principles, specifically the properties of equality. By consistently applying inverse operations and verifying the solution, we can confidently determine that y = 31. Understanding this process lays the groundwork for tackling more complex algebraic problems and underscores the widespread applicability of linear equations in diverse fields. Remember to always check your solution and practice regularly to strengthen your algebraic skills. The ability to solve linear equations is a valuable skill that extends beyond the classroom into many aspects of life.
Latest Posts
Latest Posts
-
How Many Revolutions Are In A Radian
Apr 02, 2025
-
The Si Unit For Energy Is
Apr 02, 2025
-
Finding The Angle Between Two Planes
Apr 02, 2025
-
What Are The Common Multiples Of 2 And 7
Apr 02, 2025
-
Ratio Of Each 90 If Ratio Is 7 3
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Solve This Equation 4y 228 352 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
