Simplify The Square Root Of 54
listenit
Mar 30, 2025 · 5 min read
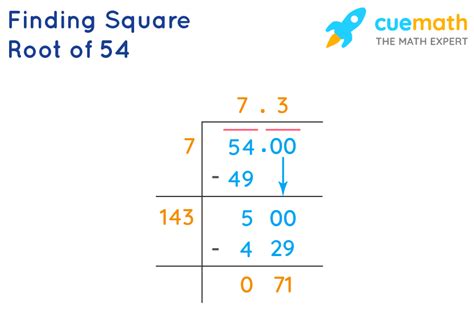
Table of Contents
Simplifying the Square Root of 54: A Comprehensive Guide
Simplifying square roots is a fundamental skill in algebra and mathematics in general. Understanding how to simplify expressions like √54 is crucial for further mathematical studies and problem-solving. This comprehensive guide will walk you through the process step-by-step, explaining the underlying concepts and providing you with practical examples to solidify your understanding. We'll also explore some common mistakes to avoid, ensuring you develop a confident and accurate approach to simplifying square roots.
Understanding Square Roots and Prime Factorization
Before diving into simplifying √54, let's refresh our understanding of square roots and a crucial tool in simplification: prime factorization.
What is a Square Root? The square root of a number (x) is a value that, when multiplied by itself, equals x. For example, the square root of 9 (√9) is 3, because 3 × 3 = 9.
Prime Factorization: This is the process of expressing a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). Prime factorization is essential for simplifying square roots because it allows us to identify perfect square factors.
Simplifying √54: A Step-by-Step Approach
Let's break down the simplification of √54 using prime factorization:
-
Find the Prime Factorization of 54: We start by finding the prime factors of 54. We can do this using a factor tree:
54 / \ 2 27 / \ 3 9 / \ 3 3Therefore, the prime factorization of 54 is 2 × 3 × 3 × 3, or 2 × 3³.
-
Identify Perfect Squares: Now, look for pairs of identical prime factors. In the prime factorization of 54 (2 × 3 × 3 × 3), we have a pair of 3s (3 × 3 = 3²).
-
Simplify Using Perfect Squares: We can rewrite 54 as a product of its perfect square factor and remaining factors:
√54 = √(2 × 3² × 3) = √(3² × (2 × 3)) = √(9 × 6)
-
Separate the Square Root: We can now separate the square root into two separate square roots:
√(9 × 6) = √9 × √6
-
Simplify the Perfect Square: We know that √9 = 3. Therefore:
3 × √6
-
Final Simplified Form: The simplified form of √54 is 3√6.
Alternative Approach Using Exponents
Another way to approach simplifying square roots involves using exponents and the properties of radicals:
-
Prime Factorization (using exponents): As before, find the prime factorization of 54: 2 × 3³.
-
Rewrite using exponents: We can write this as 2¹ × 3³.
-
Apply the radical rule: Remember that √(a * b) = √a * √b. Also remember that √a² = a. Using this, we get:
√(2¹ × 3³) = √(2¹ × 3² × 3¹) = √(3²) × √(2 × 3) = 3√6
This method is particularly helpful when dealing with larger numbers and more complex prime factorizations.
Common Mistakes to Avoid
Several common mistakes can hinder the simplification process. Let's highlight a few:
-
Incorrect Prime Factorization: An inaccurate prime factorization will lead to an incorrect simplification. Double-check your factorization to ensure all factors are prime.
-
Forgetting to Pair Factors: When looking for perfect squares, remember to only pair identical factors. A single 2 cannot be simplified, while a pair of 2s (2²) can be simplified to 2.
-
Incorrect Application of Radical Rules: Misunderstanding or misapplying rules such as √(a * b) = √a * √b can lead to errors. Make sure you understand these rules completely.
-
Not Fully Simplifying: After identifying and simplifying the perfect squares, ensure you have simplified the expression to its most basic form. For instance, √12 simplifies to 2√3, not just √4 × √3.
Practical Applications and Further Exploration
Simplifying square roots is more than just an abstract mathematical exercise. It has practical applications in various fields:
-
Geometry: Calculating lengths of sides or diagonals in geometric figures frequently involves simplifying square roots.
-
Physics: Many physics formulas include square roots, particularly those dealing with speed, distance, and energy calculations.
-
Engineering: Engineering problems often involve calculations that lead to square roots, particularly in structural analysis and design.
-
Computer Graphics: Square roots are used extensively in 3D graphics and game development for calculations related to distances and rotations.
Advanced Simplification Techniques
While the basic method outlined above covers most cases, more advanced techniques can be used to simplify more complex expressions involving square roots:
-
Rationalizing the Denominator: This technique is used to remove square roots from the denominator of a fraction. For example, to simplify 1/√2, you multiply the numerator and denominator by √2 to get √2/2.
-
Adding and Subtracting Square Roots: You can only add or subtract square roots with the same radicand (the number under the square root). For example, 2√3 + 5√3 = 7√3.
-
Multiplying and Dividing Square Roots: When multiplying or dividing square roots, you can multiply or divide the radicands. For example, √2 × √3 = √6, and √6 / √2 = √3.
Conclusion: Mastering Square Root Simplification
Mastering the simplification of square roots, like simplifying √54, is a cornerstone of mathematical proficiency. By understanding prime factorization, applying the rules of radicals correctly, and practicing regularly, you'll develop a strong foundation for more advanced mathematical concepts and real-world applications. Remember to avoid common mistakes, explore advanced techniques, and appreciate the widespread relevance of this seemingly basic mathematical skill. Consistent practice and attention to detail are key to becoming confident and accurate in simplifying square roots and other mathematical expressions. This guide provides a robust foundation for your continued learning and success in mathematics.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 10 14
Apr 01, 2025
-
What Is 6 To The Power Of 0
Apr 01, 2025
-
What Is The Oxidation State Of S In H2so4
Apr 01, 2025
-
Why Is Water A Liquid At Room Temp
Apr 01, 2025
-
Is The Number Zero A Rational Number
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
