What Is 6 To The Power Of 0
listenit
Apr 01, 2025 · 5 min read
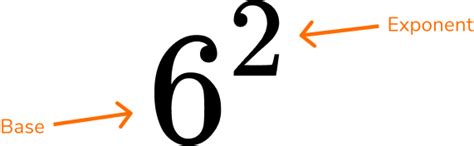
Table of Contents
What is 6 to the Power of 0? Unraveling the Mystery of Exponents
The seemingly simple question, "What is 6 to the power of 0?" often trips up even those comfortable with basic arithmetic. While the answer itself is straightforward – 1 – the underlying mathematical principles behind it require a deeper understanding of exponents and their properties. This article delves into the intricacies of this seemingly simple calculation, explaining not just the answer but also why it's the answer, exploring the rules of exponents, and dispelling common misconceptions.
Understanding Exponents: A Quick Refresher
Before tackling 6<sup>0</sup>, let's revisit the fundamentals of exponents. An exponent (also called a power or index) indicates how many times a number (the base) is multiplied by itself. For instance:
- 6<sup>1</sup> = 6 (6 multiplied by itself once)
- 6<sup>2</sup> = 6 x 6 = 36 (6 multiplied by itself twice)
- 6<sup>3</sup> = 6 x 6 x 6 = 216 (6 multiplied by itself three times)
- 6<sup>4</sup> = 6 x 6 x 6 x 6 = 1296 (6 multiplied by itself four times)
Notice a pattern? As the exponent increases by one, the result is multiplied by the base (6, in this case). This consistent pattern allows us to extrapolate and understand what happens when the exponent decreases.
The Rule of Decreasing Exponents: The Pattern Unveiled
Let's reverse the process and see what happens as we decrease the exponent:
- 6<sup>4</sup> = 1296
- 6<sup>3</sup> = 1296 / 6 = 216
- 6<sup>2</sup> = 216 / 6 = 36
- 6<sup>1</sup> = 36 / 6 = 6
Following this pattern, what would 6<sup>0</sup> be? Continuing the sequence, we divide the previous result by the base:
- 6<sup>0</sup> = 6 / 6 = 1
This demonstrates a clear pattern: dividing by the base each time the exponent decreases by one. This consistent logic leads us to the fundamental rule that anything (except zero) raised to the power of zero equals one.
The Mathematical Justification: Preserving Consistency
The above pattern provides an intuitive understanding. However, a more rigorous mathematical explanation involves maintaining the consistency of exponent rules. Consider the following exponent rule:
x<sup>a</sup> / x<sup>b</sup> = x<sup>(a-b)</sup>
Let's apply this rule with 'a' as a positive integer and 'b' as 'a':
x<sup>a</sup> / x<sup>a</sup> = x<sup>(a-a)</sup> = x<sup>0</sup>
Since any number divided by itself equals 1 (except for zero), we have:
x<sup>a</sup> / x<sup>a</sup> = 1
Therefore, x<sup>0</sup> = 1. This algebraic manipulation demonstrates that defining x<sup>0</sup> as 1 maintains consistency within the established rules of exponents, ensuring the mathematical framework remains coherent and predictable.
Why isn't 0<sup>0</sup> defined? The Case of the Indeterminate Form
While x<sup>0</sup> = 1 for any non-zero x, the case of 0<sup>0</sup> presents a unique challenge. This is because it leads to an indeterminate form in mathematics. Consider these two limiting cases:
- Limit as x approaches 0 of x<sup>x</sup>: This limit evaluates to 1.
- Limit as x approaches 0 of 0<sup>x</sup>: This limit evaluates to 0.
The conflicting results from these approaches highlight the ambiguity surrounding 0<sup>0</sup>. It's not that 0<sup>0</sup> equals something; rather, it's considered undefined because it lacks a consistent and universally agreed-upon value.
Real-world Applications: Where Does This Matter?
While the concept of 6<sup>0</sup> might seem purely theoretical, it has practical implications across various fields:
-
Computer Science: In algorithms and data structures, the zeroth power is often used in iterative calculations and combinatorial problems.
-
Physics and Engineering: Many formulas and equations in physics and engineering involve exponents, and understanding the behavior of exponents at zero is crucial for accurate calculations.
-
Finance and Economics: Compound interest calculations, for example, can involve exponents, and the understanding of 0<sup>0</sup> is important in certain scenarios.
-
Statistics and Probability: Probability calculations often involve exponents and factorials (which inherently involve exponents), and the rules concerning zero exponents are fundamental for accuracy.
Common Misconceptions and Addressing Them
Some common misconceptions about exponents, particularly regarding zero exponents, include:
-
Assuming 6<sup>0</sup> is 0: This is a frequent mistake. Remember, the pattern of dividing by the base leads to 1, not 0.
-
Misinterpreting the Rule: Students sometimes incorrectly apply the rule to zero as the base. Again, the case of 0<sup>0</sup> remains undefined.
-
Lack of Intuitive Understanding: Many struggle to visualize what raising something to the power of zero actually means. Focusing on the pattern and the consistent mathematical rules helps clarify this.
Conclusion: Mastering the Power of Zero
Understanding that 6<sup>0</sup> = 1, and more generally, that x<sup>0</sup> = 1 (for x ≠ 0), is fundamental to a solid grasp of algebra and higher-level mathematics. By understanding the patterns of exponents, the consistency of mathematical rules, and the implications of the indeterminate form 0<sup>0</sup>, we can confidently apply this knowledge to various fields and navigate more complex mathematical concepts with greater clarity. The seemingly simple question "What is 6 to the power of 0?" leads us to a deeper appreciation of the elegance and consistency within the world of mathematics. Remember to always approach mathematical concepts with curiosity and a thirst for understanding the underlying principles. This approach ensures that seemingly simple questions lead to deeper learning and a more robust mathematical foundation.
Latest Posts
Latest Posts
-
What Is The Reciprocal Of 2 5
Apr 02, 2025
-
What Is The Fraction Of 0 05
Apr 02, 2025
-
If Pressure Increases What Happens To Volume
Apr 02, 2025
-
Lowest Common Denominator Of 7 And 8
Apr 02, 2025
-
What Is 21 30 As A Percent
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
