Simplify The Square Root Of 512
listenit
Mar 31, 2025 · 4 min read
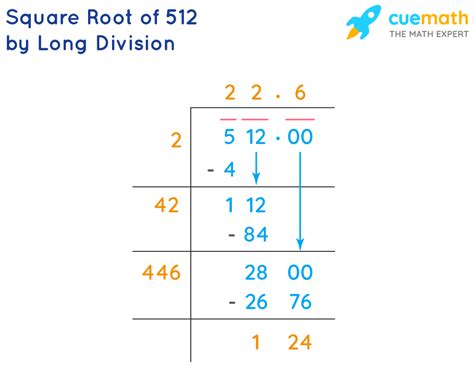
Table of Contents
Simplifying the Square Root of 512: A Comprehensive Guide
The seemingly simple task of simplifying the square root of 512 (√512) offers a fantastic opportunity to delve into the fundamentals of square roots, prime factorization, and radical simplification. This comprehensive guide will walk you through the process step-by-step, exploring different approaches and highlighting key mathematical concepts. We'll cover not only how to simplify √512 but also provide you with the tools and understanding to tackle other similar problems with confidence.
Understanding Square Roots and Prime Factorization
Before we embark on simplifying √512, let's refresh our understanding of two crucial concepts:
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Square roots can be integers (whole numbers), fractions, or irrational numbers (numbers that cannot be expressed as a simple fraction).
The Importance of Prime Factorization
Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This is a cornerstone technique in simplifying square roots. By expressing a number as a product of its prime factors, we can identify perfect squares hidden within the number, making simplification much easier.
Simplifying √512: A Step-by-Step Approach
Now, let's tackle the simplification of √512 using the method of prime factorization:
1. Find the Prime Factorization of 512:
We begin by finding the prime factors of 512. We can use a factor tree or repeated division by prime numbers. Let's use repeated division:
- 512 ÷ 2 = 256
- 256 ÷ 2 = 128
- 128 ÷ 2 = 64
- 64 ÷ 2 = 32
- 32 ÷ 2 = 16
- 16 ÷ 2 = 8
- 8 ÷ 2 = 4
- 4 ÷ 2 = 2
- 2 ÷ 2 = 1
Therefore, the prime factorization of 512 is 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2<sup>9</sup>
2. Rewrite the Square Root Using the Prime Factorization:
Now, we can rewrite √512 using the prime factorization we just found:
√512 = √(2<sup>9</sup>)
3. Simplify the Square Root:
Remember that √(a x a) = a. We can simplify the square root by pairing up the prime factors:
√(2<sup>9</sup>) = √(2<sup>2</sup> x 2<sup>2</sup> x 2<sup>2</sup> x 2<sup>2</sup> x 2) = √(2<sup>2</sup>) x √(2<sup>2</sup>) x √(2<sup>2</sup>) x √(2<sup>2</sup>) x √2
Since √(2<sup>2</sup>) = 2, we can simplify further:
2 x 2 x 2 x 2 x √2 = 16√2
Therefore, the simplified form of √512 is 16√2.
Alternative Methods for Simplifying Square Roots
While the prime factorization method is highly effective, other approaches can be used to simplify square roots, particularly for numbers with easily identifiable factors.
Recognizing Perfect Squares
Sometimes, you can simplify a square root by identifying perfect square factors. For example, you might notice that 512 is divisible by 64 (8 x 8), which is a perfect square:
512 = 64 x 8
Therefore, √512 = √(64 x 8) = √64 x √8 = 8√8
However, notice that √8 can be further simplified (√8 = √(4 x 2) = 2√2), leading us back to the same simplified form: 8 x 2√2 = 16√2
Using a Calculator (with caution)
While a calculator can quickly provide a decimal approximation of √512, it doesn't directly provide the simplified radical form. Calculators are useful for checking your work but shouldn't replace the understanding of the underlying mathematical processes.
Applications and Further Exploration
Understanding square root simplification extends far beyond simple exercises. It's a fundamental skill crucial in many areas of mathematics and science, including:
- Algebra: Simplifying radical expressions is crucial for solving equations and simplifying algebraic expressions.
- Geometry: Calculating distances, areas, and volumes often involve square roots. For example, finding the length of the diagonal of a square uses the Pythagorean theorem, which involves square roots.
- Trigonometry: Many trigonometric functions and identities involve square roots.
- Calculus: Derivatives and integrals sometimes involve simplifying radical expressions.
- Physics: Many physics equations and formulas, particularly in mechanics and electromagnetism, utilize square roots.
Practice Problems
To solidify your understanding, try simplifying the following square roots using the prime factorization method:
- √72
- √192
- √288
- √1250
Remember to break each number down into its prime factors, pair up the factors to identify perfect squares, and simplify accordingly.
Conclusion
Simplifying the square root of 512, and square roots in general, is a valuable skill rooted in the understanding of prime factorization and the properties of square roots. This process, while appearing complex at first, becomes straightforward with practice and a firm grasp of the underlying mathematical principles. By mastering this technique, you'll enhance your proficiency in algebra, geometry, and other mathematical fields, opening up new avenues of learning and problem-solving. Remember to always check your work and explore different approaches to find the method that best suits your understanding and problem-solving style. The more you practice, the more confident and efficient you'll become in simplifying square roots.
Latest Posts
Latest Posts
-
How Many Square Yards In A Square Mile
Apr 01, 2025
-
Ca Oh 2 Strong Or Weak
Apr 01, 2025
-
What Are Three Parts Of Atp Molecule
Apr 01, 2025
-
How Many Right Angles Does A Quadrilateral Have
Apr 01, 2025
-
Is Magnesium A Gas Liquid Or Solid
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 512 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
