Simplify The Square Root Of 192
listenit
Mar 28, 2025 · 5 min read
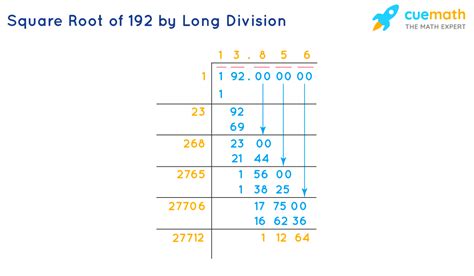
Table of Contents
Simplifying the Square Root of 192: A Comprehensive Guide
Simplifying square roots is a fundamental concept in mathematics, crucial for algebra, calculus, and various other fields. This comprehensive guide will walk you through the process of simplifying the square root of 192, explaining the underlying principles and providing practical examples. We'll cover various methods, ensuring you gain a deep understanding of this mathematical operation. By the end, you'll be able to confidently simplify other square roots with ease.
Understanding Square Roots and Simplification
Before diving into the simplification of √192, let's refresh our understanding of square roots. A square root of a number 'x' is a value that, when multiplied by itself, equals 'x'. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9.
Simplifying a square root means expressing it in its simplest radical form. This involves removing any perfect square factors from under the radical symbol (√). A perfect square is a number that results from squaring an integer (e.g., 4, 9, 16, 25, etc.). Simplifying ensures the square root is as concise and manageable as possible.
Method 1: Prime Factorization
This is the most common and reliable method for simplifying square roots. It involves breaking down the number under the radical into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Steps:
-
Find the prime factorization of 192: We can start by dividing 192 by the smallest prime number, 2: 192 ÷ 2 = 96 96 ÷ 2 = 48 48 ÷ 2 = 24 24 ÷ 2 = 12 12 ÷ 2 = 6 6 ÷ 2 = 3 Therefore, the prime factorization of 192 is 2 x 2 x 2 x 2 x 2 x 2 x 3, or 2<sup>6</sup> x 3.
-
Identify pairs of identical prime factors: Notice that we have six 2's. We can pair them up: (2 x 2) x (2 x 2) x (2 x 2) x 3.
-
Remove the pairs from under the radical: Each pair of identical prime factors can be taken out from under the square root as a single factor. This is because √(a x a) = a.
-
Simplify the expression: √192 = √(2<sup>6</sup> x 3) = √(2 x 2 x 2 x 2 x 2 x 2 x 3) = √[(2 x 2) x (2 x 2) x (2 x 2) x 3] = 2 x 2 x 2 √3 = 8√3
Therefore, the simplified form of √192 is 8√3.
Method 2: Identifying Perfect Square Factors
This method is a shortcut if you can quickly identify perfect square factors of the number. It's less systematic than prime factorization but can be faster for those proficient in recognizing perfect squares.
Steps:
-
Find a perfect square factor of 192: We know that 64 is a perfect square (8 x 8 = 64) and it's a factor of 192 (192 ÷ 64 = 3).
-
Rewrite the square root: √192 = √(64 x 3)
-
Separate the square root: √(64 x 3) = √64 x √3
-
Simplify: √64 = 8, so the expression simplifies to 8√3.
Again, we arrive at the simplified form: 8√3.
Comparing the Two Methods
Both methods achieve the same result. Prime factorization is more methodical and reliable, particularly for larger numbers where identifying perfect square factors might be challenging. The perfect square factor method is quicker if you can readily spot the perfect square factors. Choose the method you find most comfortable and efficient.
Practical Applications and Further Exploration
Simplifying square roots is not just an abstract mathematical exercise. It has numerous practical applications:
-
Geometry: Calculating areas, volumes, and lengths often involves square roots. Simplifying the square roots makes these calculations cleaner and easier to understand. For example, finding the diagonal of a square with side length 12 involves calculating √(12² + 12²) = √288 = 12√2.
-
Physics: Many physics formulas, particularly those dealing with vectors and motion, involve square roots. Simplifying square roots makes the equations easier to manipulate and solve.
-
Algebra: Simplifying square roots is essential for solving quadratic equations and simplifying algebraic expressions.
Advanced Techniques and Considerations
While the methods above are sufficient for most cases, let's consider some advanced scenarios:
-
Dealing with variables: When simplifying square roots involving variables, remember that √(x²) = |x| (the absolute value of x) to ensure the result is always non-negative.
-
Rationalizing the denominator: If you have a square root in the denominator of a fraction, it's often beneficial to rationalize the denominator by multiplying both the numerator and denominator by the square root in the denominator. This simplifies the expression and makes it easier to work with. For example, 1/√2 is rationalized to √2/2.
-
Approximating square roots: For square roots that don't simplify neatly, you can use estimation techniques or a calculator to find approximate values.
Conclusion
Simplifying the square root of 192, whether through prime factorization or identifying perfect square factors, results in the simplified form of 8√3. Mastering this skill enhances your understanding of fundamental mathematical concepts and equips you to tackle more complex problems across various fields. Remember to choose the method that best suits your comfort level and the complexity of the problem. Consistent practice will build your proficiency and confidence in simplifying square roots and other mathematical expressions. Understanding the underlying principles allows you to approach similar problems with ease and accuracy. The ability to simplify radicals is a fundamental skill that underlies numerous advanced mathematical concepts, making it a cornerstone of mathematical literacy.
Latest Posts
Latest Posts
-
What Is The Gcf Of 72 And 60
Mar 31, 2025
-
Finding The Radius Of A Circle From The Circumference
Mar 31, 2025
-
In Which Layer Does Weather Occur
Mar 31, 2025
-
What Is The Opposite Of 9
Mar 31, 2025
-
How Many Neutrons Does Carbon 13 Have
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 192 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
