Shape With 12 Edges And 6 Faces
listenit
Mar 30, 2025 · 5 min read
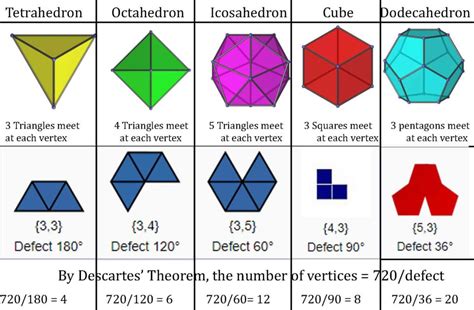
Table of Contents
Shape with 12 Edges and 6 Faces: Exploring the Octahedron
A shape with 12 edges and 6 faces is a regular octahedron. Understanding its properties, applications, and relationship to other geometric shapes is key to appreciating its significance in mathematics, science, and even art. This comprehensive guide delves deep into the world of octahedrons, providing a detailed exploration suitable for enthusiasts of all levels.
Defining the Octahedron: A Geometric Deep Dive
The octahedron, from the Greek words "ὀκτώ" (oktō) meaning "eight" and "ἕδρα" (hedra) meaning "base" or "seat," is a polyhedron composed of eight faces, twelve edges, and six vertices. The regular octahedron, possessing the highest degree of symmetry, boasts equilateral triangles for each of its eight faces. This perfect symmetry is a defining characteristic and sets it apart from other octahedral shapes.
Distinguishing Features:
- Faces: Eight equilateral triangles. This means all sides of each triangular face are equal in length.
- Edges: Twelve edges, all equal in length. Each edge connects two vertices.
- Vertices: Six vertices, where four edges meet at each point.
- Symmetry: High degree of symmetry; it exhibits rotational symmetry about various axes. This means it can be rotated in several ways while still appearing identical.
- Duality: The octahedron is the dual polyhedron of the cube. This means that connecting the centers of the faces of a cube creates an octahedron, and vice-versa.
Exploring the Mathematical Properties of the Octahedron
The mathematical properties of the octahedron are rich and extensive, offering countless opportunities for exploration and analysis. Its symmetrical nature makes it an ideal object for studying various geometric principles.
Calculating Volume and Surface Area:
The formulas for calculating the volume and surface area of a regular octahedron are relatively straightforward, relying on the length of one of its edges (often denoted as 'a'):
- Surface Area: 2√3 * a²
- Volume: (√2)/3 * a³
These formulas are readily applicable, allowing for accurate calculations based on the known edge length. Understanding these calculations is crucial for various applications, from engineering to crystallography.
Relationship to Other Platonic Solids:
The octahedron is one of the five Platonic solids, perfectly regular convex polyhedra. These solids possess exceptional symmetry and are characterized by congruent regular polygonal faces and congruent angles at each vertex. The other Platonic solids are the tetrahedron, cube, dodecahedron, and icosahedron.
The octahedron's duality with the cube highlights an important relationship between these two Platonic solids. This duality is not just a geometrical curiosity; it reflects deeper mathematical connections and symmetries.
Real-World Applications and Occurrences of Octahedrons
The octahedron's unique geometric properties lend themselves to various real-world applications and occurrences across different fields.
Crystallography and Mineralogy:
Many crystals exhibit octahedral forms. Diamond, spinel, and fluorite are notable examples of minerals that crystallize into octahedral structures. Understanding the octahedral structure is critical in crystallography for classifying and analyzing minerals.
Chemistry and Molecular Structures:
Some molecules exhibit octahedral structures, such as the sulfur hexafluoride (SF₆) molecule, where a sulfur atom is bonded to six fluorine atoms forming the shape of a perfect octahedron. This structural characteristic directly impacts chemical reactivity and properties.
Engineering and Design:
Octahedral structures offer unique advantages in engineering. Their inherent stability and strength make them suitable for various applications, including specialized components and bracing structures.
Art and Architecture:
The aesthetic appeal of the octahedron has found its way into art and architecture. The symmetry and balanced forms are often incorporated into sculptures, building designs, and artistic representations.
Constructing an Octahedron: Hands-On Activities
Building an octahedron provides a tangible understanding of its geometric properties. This hands-on approach enhances learning and allows for a deeper appreciation of the shape's unique features.
Methods of Construction:
Several methods facilitate the construction of an octahedron. These include using:
- Cardboard and glue: This is a common method requiring precise cutting and careful assembly. Templates are readily available online.
- Paper folding (origami): While requiring some skill, origami allows for a unique and aesthetically pleasing construction method.
- Computer-aided design (CAD): This method provides precise control over dimensions and allows for creation of digital models.
The chosen method will depend on available resources and skill level. However, the experience of physically constructing an octahedron provides valuable insight into its three-dimensional geometry.
Advanced Topics and Further Exploration
For those seeking a deeper understanding, several advanced topics regarding octahedrons warrant further investigation:
Truncated Octahedron:
Truncating the vertices of a regular octahedron leads to a truncated octahedron, a shape with 14 faces (6 squares and 8 hexagons), 36 edges, and 24 vertices. This shape also holds significance in crystallography and other scientific disciplines.
Octahedron in Higher Dimensions:
The concept of the octahedron can be extended to higher dimensions. The 4-dimensional analogue of the octahedron is the 16-cell, a fascinating object of study in higher-dimensional geometry.
Star Octahedron (Stella Octangula):
Two interpenetrating tetrahedrons form a star octahedron, which possesses unique symmetries and visual appeal. This creates a compound shape with a three-dimensional, visually captivating form.
Conclusion: The Enduring Allure of the Octahedron
The octahedron, with its 12 edges and 6 faces, stands as a remarkable geometric figure, captivating mathematicians, scientists, artists, and enthusiasts alike. Its symmetrical properties, mathematical elegance, and diverse applications across various disciplines highlight its enduring importance. Whether appreciating its presence in natural formations or exploring its mathematical intricacies, the octahedron remains a source of fascination and inspiration. Its study offers a rewarding journey into the world of geometry, demonstrating the beauty and interconnectedness found within mathematical structures.
Latest Posts
Latest Posts
-
Sr Oh 2 Strong Or Weak
Apr 01, 2025
-
A Bond In Which Electrons Are Shared Unequally
Apr 01, 2025
-
Greatest Common Factor Of 32 And 36
Apr 01, 2025
-
Least Common Multiple Of 4 And 30
Apr 01, 2025
-
The Principle Of Probability Can Be Used To
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Shape With 12 Edges And 6 Faces . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
