Lowest Common Multiple Of 4 And 14
listenit
Mar 28, 2025 · 5 min read
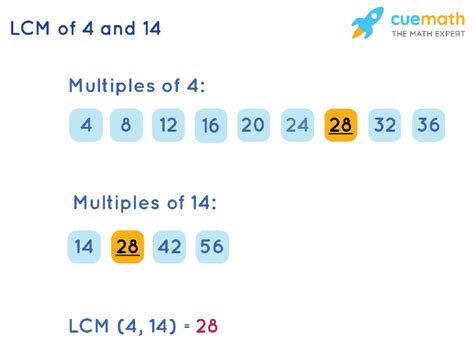
Table of Contents
Finding the Lowest Common Multiple (LCM) of 4 and 14: A Comprehensive Guide
The lowest common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to calculate the LCM is crucial for various applications, from simplifying fractions to solving complex algebraic problems. This article delves deep into the process of finding the LCM of 4 and 14, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll move beyond a simple calculation and explore the broader context of LCMs, their significance, and real-world applications.
Understanding the Lowest Common Multiple (LCM)
Before we dive into the calculation, let's clarify the definition of the LCM. The lowest common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that both (or all) numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, 14... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples are 6, 12, 18... The smallest of these common multiples is 6, therefore the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 4 and 14
There are several effective methods to determine the LCM of 4 and 14. Let's explore three common approaches:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 14: 14, 28, 42, 56...
Observing the lists, the smallest number that appears in both sequences is 28. Therefore, the LCM of 4 and 14 is 28.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 4: 2²
- Prime factorization of 14: 2 x 7
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 7: 7¹ = 7
Multiply these highest powers together: 4 x 7 = 28. Therefore, the LCM of 4 and 14 is 28.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) = (a x b) / GCD(a, b)
Let's find the GCD of 4 and 14 using the Euclidean algorithm:
- Divide 14 by 4: 14 = 4 x 3 + 2
- Divide 4 by the remainder 2: 4 = 2 x 2 + 0
The last non-zero remainder is 2, so the GCD of 4 and 14 is 2.
Now, we can use the formula:
LCM(4, 14) = (4 x 14) / 2 = 56 / 2 = 28
Therefore, the LCM of 4 and 14 is 28.
Why is Finding the LCM Important?
The LCM has numerous applications across various mathematical and real-world scenarios:
-
Simplifying Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator for simplification.
-
Solving Problems Involving Cycles: Problems involving repeating events or cycles often require the LCM to determine when events will coincide. For example, if two machines operate on cycles of 4 hours and 14 hours, respectively, the LCM (28 hours) determines when both machines will be at the same point in their cycles.
-
Scheduling and Timing: The LCM is helpful in scheduling tasks or events that need to be synchronized, such as coordinating work shifts or planning recurring events.
-
Music Theory: LCM is used in music to determine the least common multiple of the length of notes, enabling the synchronization of musical rhythms.
-
Modular Arithmetic: In cryptography and other areas of mathematics, LCM plays a critical role in understanding modular arithmetic concepts.
Expanding on the LCM Concept: More than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we simply consider all the prime factors of all the numbers and take the highest power of each. For the GCD method, it's more iterative, involving finding the GCD of two numbers at a time and progressively finding the LCM.
Visualizing the LCM
The LCM can be visualized geometrically using area models. Imagine two rectangles, one with dimensions 4 x 1 and the other with dimensions 14 x 1. To find the smallest rectangle that contains both, we need to find the smallest area that is divisible by both 4 and 14. This visual representation is especially helpful for introducing the concept to younger learners.
Conclusion: Mastering the LCM
Finding the lowest common multiple is a fundamental skill with widespread applications in various mathematical and real-world problems. Understanding the different methods – listing multiples, prime factorization, and the GCD method – empowers you to solve LCM problems efficiently, irrespective of the numbers involved. By mastering these techniques, you build a strong foundation for tackling more advanced mathematical concepts and real-world problems that require an understanding of common multiples. The LCM of 4 and 14, being 28, serves as a simple yet illustrative example of these powerful concepts and their practical implications. Remember to choose the method most suited to the numbers you are working with – for smaller numbers, the listing multiples method might be easiest, while for larger numbers, the prime factorization or GCD method offers greater efficiency.
Latest Posts
Latest Posts
-
Where Is Most Freshwater Found On Earth
Mar 31, 2025
-
Simplify The Square Root Of 512
Mar 31, 2025
-
2 1 6 As An Improper Fraction
Mar 31, 2025
-
Explain One Major Difference Between Purines And Pyrimidines
Mar 31, 2025
-
What Percent Is 1 Out Of 20
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Multiple Of 4 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
