Least Common Multiple Of 30 And 45
listenit
Apr 01, 2025 · 5 min read
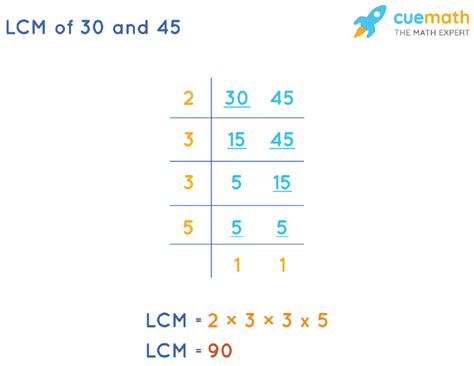
Table of Contents
Finding the Least Common Multiple (LCM) of 30 and 45: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to calculate the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article delves into the intricacies of finding the LCM of 30 and 45, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the broader applications of LCMs and their significance in various mathematical contexts.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 30 and 45, let's establish a clear definition. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors.
For instance, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 30 and 45
Several effective methods exist for calculating the LCM of two numbers. We'll explore three common approaches:
1. Listing Multiples Method
This is a straightforward, albeit potentially time-consuming method, especially for larger numbers. We list the multiples of each number until we find the smallest multiple common to both lists.
Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300...
Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360...
Observing the lists, we can see that the smallest multiple common to both is 90. Therefore, the LCM of 30 and 45 using this method is 90.
2. Prime Factorization Method
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present in the factorizations.
Prime factorization of 30:
30 = 2 × 3 × 5
Prime factorization of 45:
45 = 3² × 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹
- Highest power of 3: 3²
- Highest power of 5: 5¹
Multiplying these together: 2¹ × 3² × 5¹ = 2 × 9 × 5 = 90
Therefore, the LCM of 30 and 45 using prime factorization is 90.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This is expressed mathematically as:
LCM(a, b) × GCD(a, b) = a × b
First, we need to find the GCD of 30 and 45. We can use the Euclidean algorithm for this:
- 45 = 30 × 1 + 15
- 30 = 15 × 2 + 0
The GCD is the last non-zero remainder, which is 15.
Now we can use the formula:
LCM(30, 45) × GCD(30, 45) = 30 × 45
LCM(30, 45) × 15 = 1350
LCM(30, 45) = 1350 / 15 = 90
Therefore, the LCM of 30 and 45 using the GCD method is 90.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond abstract mathematical exercises. It finds practical applications in numerous real-world situations:
-
Scheduling: Imagine two buses that leave a station at different intervals. The LCM helps determine when both buses will depart at the same time again. For instance, if one bus departs every 30 minutes and another every 45 minutes, they will depart simultaneously again after 90 minutes.
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires calculating the LCM of the denominators. This ensures that the fractions are expressed in equivalent forms before the operation can be performed.
-
Patterning and Sequencing: In various fields like music, art, or even computer programming, cyclical patterns or sequences often emerge. The LCM can help predict when these patterns will repeat or align.
-
Gear Ratios and Mechanical Engineering: In mechanical systems with gears, the LCM is essential in determining gear ratios and synchronization of rotating components.
-
Project Management: When scheduling tasks with different completion times, LCM can be used to find the least common time when all tasks are completed.
-
Construction and Building: In tiling, flooring, or other construction work where materials are used in repetitive patterns, the LCM can help minimize waste and optimize the use of materials.
Advanced Concepts Related to LCM
Beyond the basic calculation methods, several advanced concepts are related to LCM:
-
LCM of more than two numbers: The principles discussed above can be extended to find the LCM of three or more numbers. The prime factorization method is particularly useful in these cases.
-
LCM and GCD relationship: As demonstrated earlier, the strong relationship between LCM and GCD provides an alternative and efficient method for calculating the LCM. Understanding this relationship is fundamental to number theory.
-
Applications in abstract algebra: The concept of LCM finds applications in more advanced mathematical fields, such as abstract algebra, where it is generalized to other algebraic structures beyond integers.
Conclusion: The Importance of Understanding LCM
The ability to calculate the least common multiple is a valuable skill across various mathematical disciplines and real-world applications. Understanding the different methods for calculating the LCM, such as listing multiples, prime factorization, and using the GCD relationship, allows for flexibility and efficiency in problem-solving. This article has comprehensively explored these methods, providing a solid foundation for understanding and applying this fundamental concept. The examples and real-world applications highlighted emphasize the broader importance of mastering the LCM in various contexts, demonstrating its relevance beyond abstract mathematical exercises. Remember that practice is key; the more you work with LCM problems, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
18 Is What Percent Of 27
Apr 02, 2025
-
Explain The Relationship Between Monomers And Polymers
Apr 02, 2025
-
Lowest Common Multiple Of 2 And 3 And 7
Apr 02, 2025
-
Find X Intercepts Of A Parabola
Apr 02, 2025
-
What Is 3 As A Percentage Of 25
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 30 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
