What Is 3 As A Percentage Of 25
listenit
Apr 02, 2025 · 5 min read
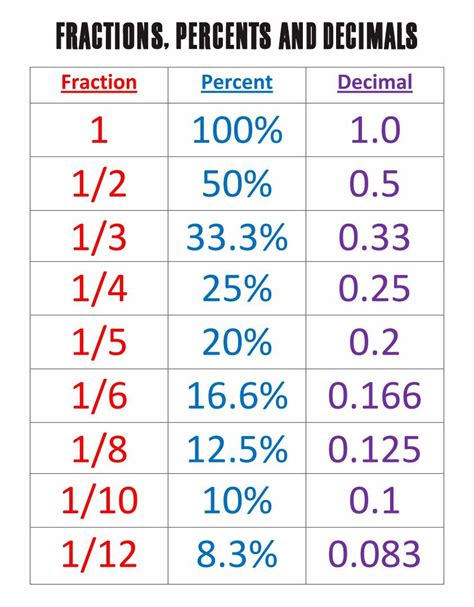
Table of Contents
What is 3 as a Percentage of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with widespread applications in various aspects of life, from calculating discounts and interest rates to analyzing data and understanding statistical information. This article delves into the specific question of "What is 3 as a percentage of 25?" while providing a broader understanding of percentage calculations. We'll explore different methods for solving this problem and offer practical examples to solidify your comprehension.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Percentages are used extensively because they offer a standardized and easily comparable way to represent proportions.
Method 1: Using the Basic Percentage Formula
The most straightforward method to calculate what percentage 3 represents of 25 is using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 3 (the number we want to express as a percentage)
- Whole: 25 (the total number)
Substituting these values into the formula:
(3 / 25) x 100% = 12%
Therefore, 3 is 12% of 25.
Method 2: Converting to a Decimal
An alternative approach involves first converting the fraction 3/25 into a decimal and then multiplying by 100% to express it as a percentage.
- Divide the part by the whole: 3 ÷ 25 = 0.12
- Multiply by 100%: 0.12 x 100% = 12%
This method yields the same result: 3 is 12% of 25.
Method 3: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion to find the unknown percentage:
3/25 = x/100
To solve for 'x' (the percentage), we can cross-multiply:
25x = 300
x = 300 / 25
x = 12
Therefore, 3 is 12% of 25.
Real-World Applications of Percentage Calculations
Understanding percentage calculations has numerous practical applications in everyday life and various professional fields. Here are a few examples:
1. Finance and Budgeting:
- Calculating interest rates: Banks and financial institutions use percentages to determine interest on loans, savings accounts, and credit cards.
- Determining discounts and sales tax: Stores use percentages to advertise sales and calculate sales tax on purchases. For example, a 20% discount on a $50 item would reduce the price by $10 (20% of $50).
- Analyzing investment returns: Investors use percentages to track the performance of their investments and assess profitability.
2. Data Analysis and Statistics:
- Representing proportions: Percentages are essential for representing proportions within datasets, making it easier to compare and interpret data. For example, the percentage of students who passed an exam or the percentage market share of a company.
- Calculating statistical measures: Percentages are used in various statistical calculations, such as calculating percentages of change or growth rates.
3. Everyday Life:
- Calculating tips: People frequently use percentages to calculate tips in restaurants or for service providers. A 15% tip on a $20 meal would be $3.
- Understanding nutritional information: Food labels often display nutritional information as percentages of recommended daily values.
- Comparing prices: Percentages can help compare the prices of different products or services, particularly when considering discounts or sales.
Beyond the Basics: More Complex Percentage Problems
While the problem "What is 3 as a percentage of 25?" is relatively straightforward, percentage calculations can become more complex. Here are some examples of more challenging scenarios:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values. For example, if a stock price increases from $10 to $12, the percentage increase is 20%.
- Finding the original value after a percentage change: This requires working backward from a final value and a percentage change to determine the initial value. For instance, if a product is sold for $60 after a 25% discount, the original price was $80.
- Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest, resulting in exponential growth.
Solving these more complex problems often requires a deeper understanding of algebraic manipulations and the use of formulas.
Practical Tips for Mastering Percentage Calculations
Here are some practical tips to help you improve your skills in percentage calculations:
- Practice regularly: The more you practice, the more comfortable you'll become with the concepts and techniques involved.
- Use different methods: Try solving problems using different methods (e.g., the basic formula, decimal conversion, proportions) to enhance your understanding and find the approach that suits you best.
- Visual aids: Utilize visual aids like charts and diagrams to represent percentage data and make it easier to grasp.
- Real-world applications: Apply your knowledge to real-world situations to make learning more engaging and relevant.
- Utilize online resources and calculators: Numerous online resources and calculators are available to assist you in performing percentage calculations, especially for more complex problems. However, it’s crucial to understand the underlying principles before relying solely on these tools.
Conclusion: Mastering the Art of Percentages
Understanding percentages is a critical skill applicable across a vast array of situations. The simple question of "What is 3 as a percentage of 25?" serves as a starting point for exploring the broader world of percentage calculations. By mastering various methods and practicing regularly, you can confidently tackle more complex percentage problems and apply this knowledge effectively in your daily life, academic pursuits, and professional endeavors. Remember that consistent practice and a deep understanding of the underlying principles are key to becoming proficient in percentage calculations.
Latest Posts
Latest Posts
-
Friction Is A Non Conservative Force
Apr 03, 2025
-
What Percent Of 27 Is 18
Apr 03, 2025
-
Whats The Square Root Of 500
Apr 03, 2025
-
How Many Feet Is 1 2 Miles
Apr 03, 2025
-
How Many Pounds In One Pint
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 As A Percentage Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
