Identify The Three Quantum Numbers For This Orbital
listenit
Apr 01, 2025 · 6 min read
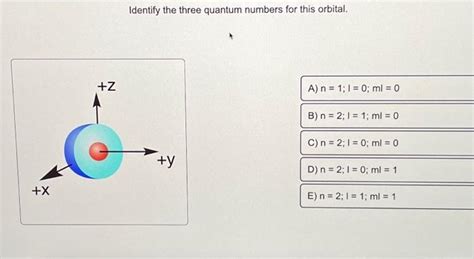
Table of Contents
Identifying the Three Quantum Numbers for a Given Orbital
Understanding atomic orbitals and their associated quantum numbers is fundamental to grasping the behavior of electrons within an atom. This article delves deep into the concept of quantum numbers, explaining how to identify the three principal quantum numbers (n, l, and ml) for any given orbital. We will explore each quantum number individually, highlighting their significance and illustrating their application with examples. Finally, we'll discuss the limitations of these three quantum numbers and the need for a fourth, the spin quantum number (ms).
What are Quantum Numbers?
Quantum numbers are a set of numerical values that describe the properties of atomic orbitals and the electrons within them. They arise from the solution of the Schrödinger equation for the hydrogen atom, a cornerstone of quantum mechanics. These numbers provide a concise and powerful way to characterize the energy, shape, and orientation of an electron's wave function. They're not arbitrary; they're dictated by the fundamental laws governing the quantum world.
The Three Principal Quantum Numbers:
-
Principal Quantum Number (n): This is the most important quantum number, determining the energy level of an electron. It dictates the electron's distance from the nucleus and the size of the orbital. 'n' can only be a positive integer (1, 2, 3, ...). Higher values of 'n' indicate higher energy levels and larger orbitals, meaning the electron is further from the nucleus and less tightly bound. For example:
- n = 1: Ground state energy level (closest to the nucleus)
- n = 2: First excited state energy level
- n = 3: Second excited state energy level, and so on.
-
Azimuthal Quantum Number (l): This number describes the shape of the orbital and its angular momentum. It's related to the principal quantum number and can have integer values ranging from 0 to (n-1). Each value of 'l' corresponds to a specific subshell:
- l = 0: s subshell (spherical shape)
- l = 1: p subshell (dumbbell shape)
- l = 2: d subshell (more complex shapes)
- l = 3: f subshell (even more complex shapes)
The number of orbitals within a subshell is determined by (2l + 1). For example, the p subshell (l=1) has three orbitals (2(1) + 1 = 3).
-
Magnetic Quantum Number (ml): This number specifies the orientation of the orbital in space. It describes the orbital's magnetic moment in the presence of an external magnetic field. The values of 'ml' can range from -l to +l, including 0. For example:
- For an s subshell (l=0), ml = 0 (only one orbital).
- For a p subshell (l=1), ml = -1, 0, +1 (three orbitals oriented along the x, y, and z axes).
- For a d subshell (l=2), ml = -2, -1, 0, +1, +2 (five orbitals).
Identifying the Quantum Numbers for Specific Orbitals:
Let's illustrate how to identify these three quantum numbers for various orbitals:
Example 1: The 1s orbital
- The "1" indicates the principal quantum number (n = 1). This means it's in the ground state energy level.
- The "s" indicates the azimuthal quantum number (l = 0). This signifies a spherical orbital.
- Since l = 0, the magnetic quantum number (ml) can only be 0. There's only one possible orientation for an s orbital.
Therefore, the quantum numbers for the 1s orbital are: n = 1, l = 0, ml = 0.
Example 2: A 2p orbital
- The "2" indicates the principal quantum number (n = 2), signifying the first excited state.
- The "p" indicates the azimuthal quantum number (l = 1). This shows a dumbbell-shaped orbital.
- Since l = 1, the magnetic quantum number (ml) can be -1, 0, or +1. Each of these values corresponds to a different spatial orientation of the 2p orbital (px, py, and pz).
Thus, a 2p orbital can have the following sets of quantum numbers:
- n = 2, l = 1, ml = -1 (2px)
- n = 2, l = 1, ml = 0 (2py)
- n = 2, l = 1, ml = +1 (2pz)
Example 3: A 3d orbital
- The "3" represents n = 3, the second excited state.
- The "d" indicates l = 2, signifying a more complex orbital shape.
- With l = 2, ml can take on values of -2, -1, 0, +1, +2. This corresponds to the five 3d orbitals with various orientations.
The Significance of Quantum Numbers in Chemistry:
The quantum numbers are not just abstract concepts; they have profound implications for understanding chemical behavior:
- Electron Configuration: Quantum numbers determine the electron configuration of an atom, which dictates its chemical properties and reactivity. The Pauli Exclusion Principle states that no two electrons in an atom can have the same set of four quantum numbers (including the spin quantum number).
- Bonding: The shapes and orientations of orbitals described by quantum numbers are crucial in understanding how atoms form chemical bonds. Overlap of orbitals leads to the formation of covalent bonds.
- Spectroscopy: Transitions of electrons between energy levels (determined by 'n') are responsible for the absorption and emission of light, which are studied in spectroscopy. This provides valuable information about the structure and composition of matter.
- Periodic Trends: Quantum numbers explain the periodic trends observed in the periodic table, such as atomic size, ionization energy, and electronegativity.
Limitations of the First Three Quantum Numbers and the Spin Quantum Number (ms):
While n, l, and ml provide a good description of the spatial properties of an electron, they don't completely describe its behavior. The fourth quantum number, the spin quantum number (ms), is needed to fully characterize an electron's state. This quantum number describes the intrinsic angular momentum of the electron, often visualized as its "spin." It can only have two values: +1/2 (spin up) or -1/2 (spin down). This is crucial because the Pauli Exclusion Principle incorporates the spin quantum number, ensuring that no two electrons in an atom can share the same four quantum numbers.
Conclusion:
The three principal quantum numbers – principal quantum number (n), azimuthal quantum number (l), and magnetic quantum number (ml) – provide a powerful framework for understanding the properties of atomic orbitals. By understanding how these numbers relate to the energy, shape, and orientation of orbitals, we can gain a deep insight into the electronic structure of atoms and the chemical properties that arise from this structure. Remember, though, that a complete description of an electron requires the inclusion of the spin quantum number (ms). The accurate determination and application of these quantum numbers are critical for advanced study in chemistry, physics, and materials science. Mastering these concepts lays the groundwork for understanding more complex quantum phenomena.
Latest Posts
Latest Posts
-
In A Hypertonic Solution A Cell Will
Apr 02, 2025
-
How Many Kilograms Are In 5000 Grams
Apr 02, 2025
-
Solve This Inequality 3b 7 32
Apr 02, 2025
-
Number Of Valence Electrons In Ar
Apr 02, 2025
-
What Is 5 9 In Decimal Form
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Identify The Three Quantum Numbers For This Orbital . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
