How To Multiply A Whole Number By A Square Root
listenit
Mar 26, 2025 · 5 min read
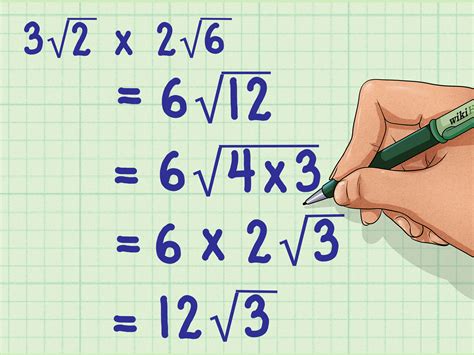
Table of Contents
How to Multiply a Whole Number by a Square Root: A Comprehensive Guide
Multiplying a whole number by a square root might seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide breaks down the process step-by-step, covering various scenarios and offering practical examples to solidify your understanding. We'll explore different approaches, emphasizing the importance of simplification and accuracy. Whether you're a student tackling algebra or an adult brushing up on your math skills, this guide will equip you with the knowledge to confidently multiply whole numbers by square roots.
Understanding the Basics: Whole Numbers and Square Roots
Before diving into the multiplication process, let's review the fundamental concepts.
What is a Whole Number?
A whole number is a non-negative number without any fractions or decimals. These include 0, 1, 2, 3, and so on. They represent complete units and are the foundation of many mathematical operations.
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Square roots can be whole numbers (like √9 = 3), decimals (like √2 ≈ 1.414), or even irrational numbers (like √2, which continues infinitely without repeating).
Multiplying a Whole Number by a Square Root: The Process
The core principle of multiplying a whole number by a square root is straightforward: treat the whole number as a coefficient. Let's explore this with some examples.
Example 1: Simple Multiplication
Let's multiply 5 by √4.
- Rewrite the expression: 5 * √4
- Calculate the square root: √4 = 2
- Perform the multiplication: 5 * 2 = 10
Therefore, 5 * √4 = 10.
Example 2: Square Root of a Non-Perfect Square
Now, let's consider a scenario with a non-perfect square: Multiply 7 by √2.
- Rewrite the expression: 7 * √2
- Since √2 is an irrational number (approximately 1.414), we approximate: 7 * 1.414 ≈ 9.898
- Depending on the required level of precision, you can round the answer: Approximately 9.9 or 10 (depending on context)
Therefore, 7 * √2 ≈ 9.898. It's crucial to note the use of the approximation symbol (≈) because √2 is an irrational number and its decimal representation goes on forever.
Example 3: Simplifying Before Multiplying
Sometimes, you can simplify the square root before performing the multiplication, making the calculation easier. Let's take 6 * √12 as an example:
- Rewrite the expression: 6 * √12
- Simplify the square root: √12 can be simplified because 12 contains a perfect square factor (4). √12 = √(4 * 3) = √4 * √3 = 2√3
- Perform the multiplication: 6 * 2√3 = 12√3
Therefore, 6 * √12 = 12√3. This simplified form is generally preferred in mathematics as it's more concise and accurate.
Handling More Complex Scenarios
The basic principles apply even when dealing with more complex expressions involving multiple square roots and whole numbers.
Example 4: Multiple Square Roots
Let's multiply 3 by √8 multiplied by √2
- Rewrite the expression: 3 * √8 * √2
- Simplify the square roots: Remember that √a * √b = √(ab). So, √8 * √2 = √(82) = √16 = 4
- Perform the multiplication: 3 * 4 = 12
Therefore, 3 * √8 * √2 = 12.
Example 5: Incorporating Variables
The method remains consistent even when variables are introduced. Let's consider 2x * √9x².
- Rewrite the expression: 2x * √9x²
- Simplify the square root: √9x² = √9 * √x² = 3x (assuming x is non-negative)
- Perform the multiplication: 2x * 3x = 6x²
Therefore, 2x * √9x² = 6x². Note the assumption about x being non-negative is essential to avoid issues with the square root of a negative number.
Practical Applications and Real-World Examples
Multiplying whole numbers by square roots appears in numerous real-world applications, particularly in areas involving geometry and physics.
Geometry: Calculating Area
Finding the area of a square with a side length of √5 units involves multiplying the side length by itself: √5 * √5 = 5 square units. Similarly, calculating the area of a rectangle with sides of length 3 and √2 units involves multiplying 3 * √2 = 3√2 square units.
Physics: Calculating Velocity and Displacement
In physics, many formulas involving velocity, acceleration, and displacement use square roots. For instance, calculating the distance traveled under constant acceleration often involves multiplying a whole number (time) by a square root term (related to acceleration).
Tips for Mastering Multiplication with Square Roots
- Master simplifying square roots: Learning to simplify square roots is critical for efficient calculations. Practice factoring numbers to identify perfect squares.
- Approximate when necessary: For irrational square roots, use approximations to obtain numerical results, remembering to indicate that your answer is approximate.
- Use a calculator carefully: Calculators can assist, but make sure you understand the underlying mathematical process; relying solely on a calculator can hinder your understanding.
- Practice regularly: Consistent practice is key to mastering any mathematical concept. Work through various examples to build your confidence and proficiency.
- Understand the order of operations (PEMDAS/BODMAS): Ensure you apply the order of operations correctly when dealing with more complex expressions involving multiple operations.
Conclusion: Embracing the Power of Square Roots
Multiplying whole numbers by square roots is a fundamental mathematical operation with widespread applications. By understanding the basic principles, practicing simplification techniques, and applying the appropriate approximations, you can confidently tackle these calculations in various contexts. This guide has provided a thorough exploration of the topic, equipping you with the necessary tools and knowledge to master this important skill. Remember that consistent practice is the key to achieving mastery, so continue to work through examples and expand your understanding. Remember to always check your work and ensure your answers are correctly simplified. With dedication and practice, you’ll become proficient in multiplying whole numbers by square roots and confidently apply this knowledge to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
60 Is 20 Of What Number
Mar 27, 2025
-
Find The Product Of 543 1187 And 100
Mar 27, 2025
-
What Percent Of 400 Is 48
Mar 27, 2025
-
Is Freezing Water Endothermic Or Exothermic
Mar 27, 2025
-
Delta H Is Negative Exothermic Or Endothermic
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about How To Multiply A Whole Number By A Square Root . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
