60 Is 20 Of What Number
listenit
Mar 27, 2025 · 5 min read
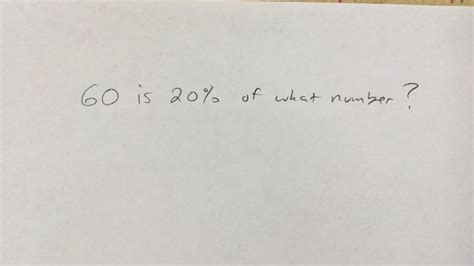
Table of Contents
60 is 20% of What Number? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "60 is 20% of what number?", opens the door to a fascinating exploration of percentages, their applications, and how to solve various percentage-related problems. Understanding percentages is crucial in numerous aspects of life, from calculating discounts and taxes to analyzing financial reports and understanding statistical data. This article will not only answer the core question but will also provide you with a robust understanding of percentage calculations, equipping you with the tools to tackle similar problems with confidence.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per cent). So, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20.
Understanding this fundamental concept is key to solving percentage problems. We can express percentages in three ways:
- Fraction: 20/100 (simplifies to 1/5)
- Decimal: 0.20
- Percentage: 20%
Solving "60 is 20% of What Number?"
Now, let's tackle the core question: "60 is 20% of what number?" We can solve this using several methods. Each method offers a different approach, helping to build a comprehensive understanding of percentage calculations.
Method 1: Using the Equation
The most straightforward method involves setting up an equation. Let's represent the unknown number as 'x'. The problem can be translated into the following equation:
0.20 * x = 60
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.20:
x = 60 / 0.20
x = 300
Therefore, 60 is 20% of 300.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion as follows:
20/100 = 60/x
This proportion states that the ratio of 20 to 100 is equal to the ratio of 60 to the unknown number (x). To solve for x, we can cross-multiply:
20 * x = 60 * 100
20x = 6000
x = 6000 / 20
x = 300
Again, we find that 60 is 20% of 300.
Method 3: Using the Percentage Formula
A more general formula for percentage calculations is:
(Part / Whole) * 100 = Percentage
In our problem, we know the "Part" (60) and the "Percentage" (20%). We need to find the "Whole" (x). We can rearrange the formula to solve for the "Whole":
Whole = (Part / Percentage) * 100
Substituting the known values:
Whole = (60 / 20) * 100
Whole = 3 * 100
Whole = 300
Once again, the solution is 300.
Expanding on Percentage Calculations: Real-World Applications
The ability to perform percentage calculations is invaluable in numerous real-world situations. Here are a few examples:
1. Calculating Discounts:
Imagine a store offering a 30% discount on an item originally priced at $150. To calculate the discount amount:
Discount = 30% of $150 = 0.30 * $150 = $45
The discounted price would be $150 - $45 = $105.
2. Determining Tax Amounts:
If a sales tax rate is 8%, and you purchase an item for $75, the tax amount would be:
Tax = 8% of $75 = 0.08 * $75 = $6
The total cost, including tax, would be $75 + $6 = $81.
3. Analyzing Financial Statements:
Percentage changes are frequently used in financial analysis. For example, if a company's revenue increased from $1 million to $1.2 million, the percentage increase would be:
Percentage Increase = [(1.2 million - 1 million) / 1 million] * 100 = 20%
4. Understanding Statistical Data:
Percentages are essential for interpreting statistical data. For example, if a survey shows that 65% of respondents prefer a particular product, it indicates that out of 100 respondents, 65 preferred that product.
Beyond the Basics: More Complex Percentage Problems
While the initial problem was relatively straightforward, percentage calculations can become more complex. Here are some examples:
1. Finding the Percentage Increase or Decrease:
These calculations involve determining the percentage change between two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
A positive value indicates an increase, while a negative value indicates a decrease.
2. Calculating Percentage Points:
Percentage points represent the absolute difference between two percentages. For example, if the interest rate increases from 5% to 8%, the increase is 3 percentage points, not 3%. This distinction is crucial in financial contexts.
3. Compound Interest Calculations:
Compound interest involves earning interest on both the principal amount and accumulated interest. The formula is more complex and involves exponential growth.
Mastering Percentage Calculations: Tips and Tricks
Mastering percentage calculations takes practice. Here are some tips:
- Practice regularly: Solve various percentage problems to build your understanding and speed.
- Understand the concepts: Focus on grasping the underlying principles of percentages, fractions, and decimals.
- Use different methods: Experiment with various approaches, such as the equation method, proportion method, and percentage formula, to find the method that best suits your style.
- Check your work: Always verify your answers using a different method or calculator to ensure accuracy.
- Utilize online resources: There are numerous online calculators and tutorials available to help you practice and learn more.
Conclusion
The question, "60 is 20% of what number?" serves as a springboard to explore the wide-ranging applications of percentage calculations. Understanding percentages is not just about solving mathematical problems; it’s a crucial skill for navigating everyday life, making informed financial decisions, and interpreting data effectively. By mastering these techniques and consistently practicing, you'll become proficient in handling various percentage-related challenges, empowering you to confidently analyze information and make sound judgments in numerous situations. Remember, consistent practice is the key to mastering percentage calculations. So, grab a calculator, try some practice problems, and watch your understanding grow!
Latest Posts
Latest Posts
-
How Many Protons Neutrons And Electrons Does Boron Have
Mar 30, 2025
-
How Many Sides Are There In A Dodecagon
Mar 30, 2025
-
Divides The Body Into Anterior And Posterior Sections
Mar 30, 2025
-
Lim As X Approaches Negative Infinity
Mar 30, 2025
-
How To Factor X 3 2x 2
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
