How Many Sides Are There In A Dodecagon
listenit
Mar 30, 2025 · 6 min read
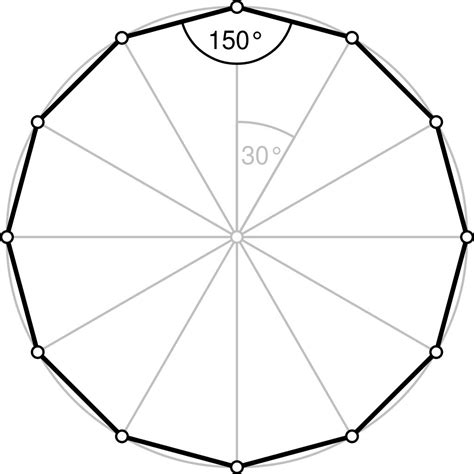
Table of Contents
How Many Sides Does a Dodecagon Have? A Deep Dive into Geometry
The question, "How many sides does a dodecagon have?" might seem simple at first glance. The answer, of course, is twelve. However, delving deeper into the fascinating world of dodecagons reveals a wealth of geometric properties and applications that extend far beyond a simple count of its sides. This article explores the dodecagon in detail, examining its characteristics, variations, and significance in various fields. We'll move beyond the basic answer and uncover the rich mathematical tapestry woven around this twelve-sided polygon.
Understanding the Dodecagon: A Definition
A dodecagon is a polygon with twelve sides and twelve angles. The word itself derives from the Greek words "dodeka," meaning twelve, and "gonia," meaning angle. This straightforward definition forms the foundation for understanding its more complex properties. It's important to note that dodecagons can be regular or irregular, significantly influencing their characteristics.
Regular vs. Irregular Dodecagons
-
Regular Dodecagon: A regular dodecagon has all twelve sides of equal length and all twelve angles of equal measure. This symmetrical nature leads to predictable and easily calculable properties. Each interior angle of a regular dodecagon measures 150 degrees, a fact we will derive later in the article.
-
Irregular Dodecagon: An irregular dodecagon, conversely, has sides and angles of varying lengths and measures. Calculating its properties becomes significantly more complex, often requiring advanced geometric techniques or computational methods. The lack of symmetry makes analysis more challenging.
Calculating the Properties of a Regular Dodecagon
The regular dodecagon offers a beautiful example of mathematical elegance. Its properties can be derived using fundamental geometric principles. Let's explore some key calculations:
Interior Angle Calculation
The sum of the interior angles of any polygon with n sides is given by the formula: (n - 2) * 180 degrees. For a dodecagon (n = 12), this sum is: (12 - 2) * 180 = 1800 degrees.
Since a regular dodecagon has equal interior angles, each angle measures: 1800 degrees / 12 = 150 degrees.
Exterior Angle Calculation
The exterior angle of any polygon is the supplementary angle to its interior angle. Therefore, the exterior angle of a regular dodecagon is: 180 degrees - 150 degrees = 30 degrees. The sum of the exterior angles of any polygon always equals 360 degrees. This is a fundamental property used in many geometric proofs.
Area Calculation
Calculating the area of a regular dodecagon requires a more nuanced approach. One common method involves dividing the dodecagon into twelve congruent isosceles triangles, each with one vertex at the center of the dodecagon. The area of each triangle can then be calculated, and multiplied by twelve to obtain the total area. The formula utilizes the side length (s) of the dodecagon:
Area = 3(2 + √3) * s²
This formula elegantly demonstrates the relationship between the side length and the area of the regular dodecagon.
Applications of Dodecagons
The twelve-sided figure, despite its seemingly simple structure, finds applications in various fields:
Architecture and Design
Dodecagons, particularly regular dodecagons, appear in architectural designs for their aesthetic appeal and structural stability. While not as common as squares or hexagons, their unique shape can create visually interesting and distinctive structures. Think of intricate floor patterns, ceiling designs, or even the overall shape of certain buildings incorporating dodecagonal elements.
Art and Tessellations
The regular dodecagon, with its twelve-fold symmetry, provides a rich source of inspiration for artists and designers. Its ability to be incorporated into tessellations – repeating patterns that cover a surface without gaps or overlaps – adds to its appeal. This makes it suitable for creating visually stunning and complex designs in various artistic mediums.
Nature and Crystals
While less prevalent than other shapes in naturally occurring formations, dodecagonal symmetry can be observed in certain crystal structures and natural patterns. The precise angles and symmetries present in a regular dodecagon resonate with principles found in nature's designs, even if not always directly manifested.
Games and Puzzles
Dodecagons also find their way into games and puzzles, often leveraging their unique geometry to create interesting challenges. Imagine a twelve-sided die, for instance, or a puzzle involving fitting dodecagonal pieces together. The twelve-fold symmetry can introduce complexity and variety.
Exploring the Deeper Mathematics of Dodecagons
The seemingly simple question of how many sides a dodecagon has opens the door to more advanced mathematical concepts:
Trigonometry and Geometry
Calculating the various properties of a dodecagon, such as its area, perimeter, and the lengths of its diagonals, involves the application of trigonometric functions and geometric theorems. The relationships between angles, sides, and areas demonstrate the interconnectedness of these mathematical fields.
Euclidean Geometry vs. Non-Euclidean Geometry
The properties of dodecagons, as we've explored them so far, are defined within the framework of Euclidean geometry. However, the concepts of dodecagons can be extended to other geometries, such as spherical or hyperbolic geometry, where the rules and properties differ significantly. Exploring these different geometrical frameworks provides a richer understanding of the nature of shapes and space.
Advanced Geometric Constructions
Constructing a regular dodecagon using only a compass and straightedge is a classic geometric challenge. The process involves carefully dividing a circle into twelve equal parts, demonstrating the precision and elegance of classical geometric techniques. This construction highlights the relationship between geometry, algebra, and number theory.
Beyond the Twelve Sides: Relating Dodecagons to Other Polygons
Understanding the dodecagon allows for a broader appreciation of polygons in general. Its twelve sides place it within the broader family of polygons, allowing for comparisons and contrasts with other shapes:
Comparison with Other Regular Polygons
Comparing a dodecagon to other regular polygons, such as squares, hexagons, or octagons, highlights the variations in their properties. The relationships between the number of sides, the measure of interior angles, and the area provide insights into the general properties of polygons.
Relationship to the Dodecahedron
The dodecagon is closely related to the dodecahedron, a three-dimensional solid with twelve pentagonal faces. Understanding the dodecagon’s properties helps to visualize and analyze the properties of this three-dimensional shape. The connections between two-dimensional and three-dimensional shapes are a fundamental aspect of geometry.
Conclusion: The Enduring Significance of the Dodecagon
While the simple answer to the question, "How many sides does a dodecagon have?" is twelve, the journey to understanding this answer has taken us through a fascinating exploration of geometry, trigonometry, and the broader world of mathematics. From architectural designs to artistic creations and the intricacies of advanced mathematical concepts, the dodecagon reveals itself to be a shape with far more depth and significance than its simple definition might suggest. Its twelve sides serve as a gateway to a wealth of mathematical beauty and practical applications. The exploration of the dodecagon underscores the power of mathematics to illuminate the world around us and to inspire creativity and innovation.
Latest Posts
Latest Posts
-
Which Element Is Liquid At Room Temperature
Apr 01, 2025
-
All Atoms Of A Given Element Have The Same
Apr 01, 2025
-
Solve This Equation 4y 228 352
Apr 01, 2025
-
Oxidation Reactions Are Coupled With Reactions
Apr 01, 2025
-
Whats Half Of 1 And 1 2
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Sides Are There In A Dodecagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
