How To Find Width Of Rectangular Prism
listenit
Mar 31, 2025 · 5 min read
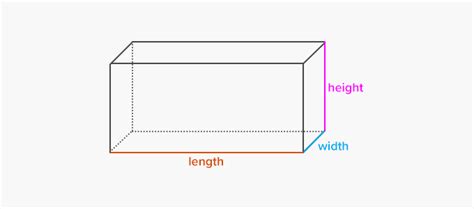
Table of Contents
How to Find the Width of a Rectangular Prism: A Comprehensive Guide
Determining the width of a rectangular prism might seem straightforward, but the approach depends heavily on the information you already possess. This comprehensive guide will walk you through various scenarios, providing clear explanations and practical examples to help you master this fundamental geometrical concept. We'll cover everything from simple direct measurements to more complex calculations using volume and surface area.
Understanding Rectangular Prisms and Their Dimensions
A rectangular prism, also known as a cuboid, is a three-dimensional shape with six rectangular faces. It has three dimensions:
- Length (l): The longest side of the rectangular base.
- Width (w): The shorter side of the rectangular base.
- Height (h): The distance between the two parallel bases.
Understanding the relationship between these dimensions is crucial for calculating any one of them, given the others.
Method 1: Direct Measurement
The simplest way to find the width of a rectangular prism is through direct measurement. This method is best suited for physical objects.
Materials Needed:
- A ruler or measuring tape
- The rectangular prism
Procedure:
- Identify the width: Visually determine which side represents the width of the prism. Remember, it's the shorter side of the rectangular base.
- Place the ruler: Align the ruler along the edge representing the width, ensuring it's parallel to the edge.
- Read the measurement: Record the measurement in the appropriate units (e.g., centimeters, inches, meters).
Example: If you measure the width of a box using a ruler and find it to be 10 centimeters, then the width of the rectangular prism is 10 cm. This method is precise if your measurements are accurate. Remember to always double-check your measurements to minimize errors.
Method 2: Using Volume
If you know the volume and the length and height of the rectangular prism, you can calculate the width using the volume formula.
Formula:
Volume (V) = Length (l) × Width (w) × Height (h)
Rearranging the formula to solve for width:
Width (w) = Volume (V) / (Length (l) × Height (h))
Example:
Let's say you have a rectangular prism with a volume of 120 cubic centimeters, a length of 6 centimeters, and a height of 4 centimeters. To find the width:
w = 120 cm³ / (6 cm × 4 cm) = 120 cm³ / 24 cm² = 5 cm
Therefore, the width of the rectangular prism is 5 centimeters. This method is especially useful when dealing with irregularly shaped prisms where direct measurement is difficult or impossible, provided you can accurately determine the volume. Keep in mind that any error in the volume measurement will directly impact the calculated width.
Method 3: Using Surface Area
The surface area of a rectangular prism is the sum of the areas of its six rectangular faces. While less direct than the volume method, you can determine the width if you know the surface area, length, and height.
Formula:
Surface Area (SA) = 2(lw + lh + wh)
This equation is more complex, and solving for 'w' requires algebraic manipulation. Let's break down the steps:
- Substitute known values: Replace SA, l, and h with their known values.
- Simplify the equation: Combine like terms and isolate the terms containing 'w'.
- Solve for 'w': Use algebraic techniques (like factoring and the quadratic formula if necessary) to solve for the width 'w'.
Example:
Suppose you have a rectangular prism with a surface area of 148 square centimeters, a length of 8 centimeters, and a height of 3 centimeters. We'll solve for the width:
148 = 2(8w + 8(3) + 3w) 148 = 2(11w + 24) 74 = 11w + 24 50 = 11w w = 50/11 ≈ 4.55 cm
Therefore, the width of the rectangular prism is approximately 4.55 centimeters. This method is less intuitive than the volume method but provides an alternative approach when surface area information is available. Accuracy heavily relies on the precision of the surface area measurement.
Method 4: Using Diagonal Measurement and Pythagorean Theorem (3D Version)
If you know the length, height, and the length of the space diagonal, you can use a 3D version of the Pythagorean theorem to find the width. The space diagonal is the longest distance between two opposite corners of the rectangular prism.
Formula:
d² = l² + w² + h² where 'd' is the space diagonal
Solving for 'w':
w² = d² - l² - h² w = √(d² - l² - h²)
Example:
Let's say the space diagonal is 13 cm, the length is 12 cm, and the height is 3 cm. To find the width:
w = √(13² - 12² - 3²) = √(169 - 144 - 9) = √16 = 4 cm
Thus, the width is 4 cm. This method requires precise measurements of the space diagonal, length, and height. Inaccuracy in any of these will propagate into the final width calculation.
Dealing with Real-World Scenarios and Potential Challenges
While the above methods provide a theoretical framework, real-world applications often present challenges:
- Measurement inaccuracies: Inherent limitations in measuring tools (rulers, tape measures) introduce errors. Multiple measurements and averaging can mitigate this.
- Irregular shapes: If the prism is not perfectly rectangular, direct measurement becomes less reliable. Consider using more sophisticated techniques or approximations.
- Complex shapes: For very complex or irregular prisms, advanced geometrical techniques (calculus, 3D modeling software) may be necessary.
- Units of measurement: Always ensure consistency in units throughout your calculations. Converting between units (e.g., inches to centimeters) is crucial for accurate results.
Advanced Techniques and Applications
For more complex scenarios, consider these advanced approaches:
- 3D scanning: Technological advancements like 3D scanners can provide highly accurate dimensions, even for irregularly shaped objects. This data can then be fed into software to calculate the width precisely.
- Computer-aided design (CAD): CAD software allows for precise modeling of rectangular prisms, enabling accurate dimension extraction.
- Image analysis: Advanced image processing techniques can extract dimensional information from high-resolution images of rectangular prisms.
Conclusion: Mastering Rectangular Prism Width Calculation
Determining the width of a rectangular prism involves a variety of methods, each suited to different scenarios and levels of information available. Understanding the fundamental principles and relationships between volume, surface area, and dimensions is key to successfully calculating the width, regardless of the approach employed. By mastering these techniques, you will gain a solid foundation in geometrical problem-solving and have the tools to tackle numerous real-world scenarios. Remember to always double-check your work and consider the potential sources of error in your measurements. The accuracy of your final answer directly depends on the accuracy of your initial data. Practice is key to developing confidence and proficiency in solving these types of geometric problems.
Latest Posts
Latest Posts
-
What Is 2 9 In A Decimal
Apr 01, 2025
-
What Is 24 Divided By 4
Apr 01, 2025
-
Milk Turning Sour Is A Chemical Change
Apr 01, 2025
-
Where On The Periodic Table Are Metals Found
Apr 01, 2025
-
What Is 0 875 In A Fraction
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find Width Of Rectangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
